Slide bài giảng Toán 12 kết nối Bài 9: Khoảng biến thiên và khoảng tứ phân vị
Slide điện tử Bài 9: Khoảng biến thiên và khoảng tứ phân vị. Kiến thức bài học được hình ảnh hóa, sinh động hóa. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 12 Kết nối tri thức sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 9: KHOẢNG BIẾN THIÊN VÀ KHOẢNG TỨ PHÂN VỊ
1. KHOẢNG BIẾN THIÊN
Hoạt động 1: Trong tình huống mở đầu, gọi ![]() là nhiệt độ cao nhất trong ngày của 30 ngày tháng Sáu năm 2021 (mẫu số liệu gốc).
là nhiệt độ cao nhất trong ngày của 30 ngày tháng Sáu năm 2021 (mẫu số liệu gốc).
- Có thể tính chính xác khoảng biến thiên cho mẫu số liệu gốc hay không?
- Giá trị lớn nhất, giá trị nhỏ nhất
 có thể nhận là gì?
có thể nhận là gì? - Hãy đưa ra một giá trị xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc.
Giải rút gọn:
- Không thể.
- Giá trị lớn nhất
 có thể nhận là 40. Giá trị nhỏ nhất
có thể nhận là 40. Giá trị nhỏ nhất  có thể nhận là 28.
có thể nhận là 28.  .
.
Luyện tập 1: Thời gian hoàn thành bài kiểm tra môn Toán của các bạn trong lớp 12C được cho trong bảng sau:
Thời gian (phút) |
|
|
|
|
Số học sinh | 8 | 16 | 4 | 2 |
- Tính khoảng biến thiên R cho mẫu số liệu ghép nhóm trên.
- Nếu biết học sinh hoàn thành bài kiểm tra sớm nhất mất 27 phút và muộn nhất mất 43 phút thì khoảng biến thiên của mẫu số liệu gốc là bao nhiêu?
Giải rút gọn:
 .
. .
.
2. KHOẢNG TỨ PHÂN VỊ
Hoạt động 2: Trong tình huống mở đầu, gọi ![]() là nhiệt độ cao nhất trong ngày của 30 ngày tháng Sáu năm 2022 (mẫu số liệu gốc).
là nhiệt độ cao nhất trong ngày của 30 ngày tháng Sáu năm 2022 (mẫu số liệu gốc).
- Có thể tính chính xác khoảng tứ phân vị của mẫu số liệu gốc hay không?
- Tìm tứ phân vị thứ nhất
 và tứ phân vị thứ ba
và tứ phân vị thứ ba  cho mẫu số liệu ghép nhóm.
cho mẫu số liệu ghép nhóm. - Hãy đưa ra một giá trị xấp xỉ cho khoảng tứ phân vị của mẫu số liệu gốc.
Giải rút gọn:
- Không thể.
- Cỡ mẫu là
 . Gọi
. Gọi  là nhiệt độ cao nhất trong ngày của 30 ngày tháng Sáu năm 2022 và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự tăng dần.
là nhiệt độ cao nhất trong ngày của 30 ngày tháng Sáu năm 2022 và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự tăng dần.
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ nhất là nhóm
nên nhóm chứa tứ phân vị thứ nhất là nhóm ![]() và tứ phân vị thứ nhất là:
và tứ phân vị thứ nhất là:
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ ba là nhóm
nên nhóm chứa tứ phân vị thứ ba là nhóm ![]() và tứ phân vị thứ ba là:
và tứ phân vị thứ ba là:

Luyện tập 2: Một người ghi lại thời gian đàm thoại của một số cuộc gọi cho kết quả như bảng sau:
Thời gian | Số cuộc gọi |
| 8 |
| 17 |
| 25 |
| 20 |
| 10 |
Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
Giải rút gọn:
| Thời gian | |||||
| Số cuộc gọi | 8 | 17 | 25 | 20 | 10 |
Cỡ mẫu là ![]() . Gọi
. Gọi ![]() là thời gian đàm thoại của 80 cuộc gọi và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự tăng dần.
là thời gian đàm thoại của 80 cuộc gọi và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự tăng dần.
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ nhất là nhóm
nên nhóm chứa tứ phân vị thứ nhất là nhóm ![]() và tứ phân vị thứ nhất là:
và tứ phân vị thứ nhất là:  .
.
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ ba là nhóm
nên nhóm chứa tứ phân vị thứ ba là nhóm ![]() và tứ phân vị thứ ba là:
và tứ phân vị thứ ba là:  .
.
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:  .
.
Vận dụng: Hãy giải bài toán trong tình huống mở đầu bằng cách sử dụng khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm.
Giải rút gọn:
Năm 2021: Khoảng biến thiên của nhiệt độ là:![]()
Cỡ mẫu là ![]() . Gọi
. Gọi ![]() là nhiệt độ cao nhất trong ngày của 30 ngày tháng Sáu năm 2021 và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
là nhiệt độ cao nhất trong ngày của 30 ngày tháng Sáu năm 2021 và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ nhất là nhóm
nên nhóm chứa tứ phân vị thứ nhất là nhóm ![]() và tứ phân vị thứ nhất là:
và tứ phân vị thứ nhất là:  .
.
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ ba là nhóm
nên nhóm chứa tứ phân vị thứ ba là nhóm ![]() và tứ phân vị thứ ba là:
và tứ phân vị thứ ba là:

Khoảng biến thiên của mẫu số liệu ghép nhóm là:
Năm 2022: Khoảng biến thiên của nhiệt độ là:![]()
Cỡ mẫu là ![]() . Gọi
. Gọi ![]() là nhiệt độ cao nhất trong ngày của 30 ngày tháng Sáu năm 2022 và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự tăng dần.
là nhiệt độ cao nhất trong ngày của 30 ngày tháng Sáu năm 2022 và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự tăng dần.
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ nhất là nhóm
nên nhóm chứa tứ phân vị thứ nhất là nhóm ![]() và tứ phân vị thứ nhất là:
và tứ phân vị thứ nhất là:
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ ba là nhóm
nên nhóm chứa tứ phân vị thứ ba là nhóm ![]() và tứ phân vị thứ ba là:
và tứ phân vị thứ ba là:

Khoảng biến thiên của mẫu số liệu ghép nhóm là:![]()
Theo khoảng biến thiên: Vì ![]() nên nhiệt độ cao nhất trong ngày vào tháng 6 năm 2022 biến đổi nhiều hơn nhiệt độ cao nhất trong ngày vào tháng 6 năm 2021.
nên nhiệt độ cao nhất trong ngày vào tháng 6 năm 2022 biến đổi nhiều hơn nhiệt độ cao nhất trong ngày vào tháng 6 năm 2021.
Theo khoảng tứ phân vị: Vì ![]() nên nhiệt độ cao nhất trong ngày vào tháng 6 năm 2021 biến đổi nhiều hơn nhiệt độ cao nhất trong ngày vào tháng 6 năm 2022.
nên nhiệt độ cao nhất trong ngày vào tháng 6 năm 2021 biến đổi nhiều hơn nhiệt độ cao nhất trong ngày vào tháng 6 năm 2022.
GIẢI BÀI TẬP
Giải rút gọn bài 3.1 trang 78 sách toán 12 tập 1 kntt
Thống kê số thẻ vàng của mỗi câu lạc bộ trong giải ngoại hạng Anh mùa giải 2021 – 2022 cho kết quả như sau:
101 | 79 | 79 | 78 | 75 | 73 | 68 | 67 | 67 | 63 |
63 | 61 | 60 | 59 | 57 | 55 | 55 | 50 | 47 | 42 |
- Hãy ghép nhóm dãy số liệu trên thành các nhóm có độ dài bằng nhau với nhóm đầu tiên là
 .
. - Tính khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu gốc và mẫu số liệu ghép nhóm thu được ở câu a. Giá trị nào là giá trị chính xác? Giá trị nào là giá trị xấp xỉ?
Giải rút gọn:
- Bảng số liệu ghép nhóm:
| Số thẻ |
|
|
|
|
|
|
|
| Tần số | 2 | 5 | 7 | 5 | 0 | 0 | 1 |
- Với mẫu số liệu gốc: Khoảng biến thiên là:
 .
.
Sắp xếp mẫu số liệu theo thứ tự không giảm là:
![]()
Vì ![]() nên tứ phân vị thứ nhất là trung vị của dãy số liệu:
nên tứ phân vị thứ nhất là trung vị của dãy số liệu:![]()
Do đó,
Tứ phân vị thứ ba là trung vị của dãy số liệu: ![]() .
.
Do đó,  .
.
Khoảng tứ phân vị là:![]()
Với mẫu số liệu ghép nhóm: Khoảng biến thiên là:![]()
Cỡ mẫu là ![]() . Gọi
. Gọi ![]() là số thẻ vàng mà mỗi câu lạc bộ ngoại hạng Anh nhận được mùa giải 2021- 2022, các giá trị này đã được sắp xếp theo thứ tự không giảm.
là số thẻ vàng mà mỗi câu lạc bộ ngoại hạng Anh nhận được mùa giải 2021- 2022, các giá trị này đã được sắp xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là  nên nhóm chứa tứ phân vị thứ nhất là nhóm
nên nhóm chứa tứ phân vị thứ nhất là nhóm ![]() và ta có:
và ta có:  .
.
Tứ phân vị thứ ba của mẫu số liệu gốc là  nên nhóm chứa tứ phân vị thứ ba là nhóm
nên nhóm chứa tứ phân vị thứ ba là nhóm ![]() và ta có:
và ta có: 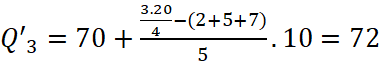 .
.
Khoảng biến thiên của mẫu số liệu ghép nhóm là:![]()
Giá trị chính xác là ![]() ;
; ![]() , giá trị xấp xỉ là
, giá trị xấp xỉ là ![]() ;
; ![]() .
.
Giải rút gọn bài 3.2 trang 79 sách toán 12 tập 1 kntt
Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:
| Thu nhập |
|
|
|
|
|
| Số người của nhà máy A | 20 | 35 | 45 | 35 | 20 |
| Số người của nhà máy B | 17 | 23 | 30 | 23 | 17 |
Tính mức thu nhập trung bình của người lao động ở hai nhà máy trên. Dựa vào khoảng tứ phân vị, hãy xác định xem mức thu nhập của người lao động ở nhà máy nào biến động nhiều hơn.
Giải rút gọn:
| Thu nhập |
|
|
|
|
|
| Giá trị đại diện | 6,5 | 9,5 | 12,5 | 15,5 | 18,5 |
| Số người của nhà máy A | 20 | 35 | 45 | 35 | 20 |
| Số người của nhà máy B | 17 | 23 | 30 | 23 | 17 |
Mức thu nhập trung bình của người lao động nhà máy A là:
 (triệu đồng)
(triệu đồng)
Mức thu nhập trung bình của người lao động nhà máy B là:
 (triệu đồng)
(triệu đồng)
Nhà máy A: Ta có cỡ mẫu ![]() . Gọi
. Gọi ![]() là mức thu nhập của người lao động nhà máy A và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
là mức thu nhập của người lao động nhà máy A và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ nhất là nhóm
nên nhóm chứa tứ phân vị thứ nhất là nhóm ![]() và tứ phân vị thứ nhất là:
và tứ phân vị thứ nhất là:
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ ba là nhóm
nên nhóm chứa tứ phân vị thứ ba là nhóm ![]() và tứ phân vị thứ ba là:
và tứ phân vị thứ ba là:

Khoảng biến thiên của mẫu số liệu ghép nhóm là:
Nhà máy B: Ta có cỡ mẫu ![]() . Gọi
. Gọi ![]() là mức thu nhập của người lao động nhà máy B và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
là mức thu nhập của người lao động nhà máy B và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ nhất là nhóm
nên nhóm chứa tứ phân vị thứ nhất là nhóm ![]() và tứ phân vị thứ nhất là:
và tứ phân vị thứ nhất là:
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ ba là nhóm
nên nhóm chứa tứ phân vị thứ ba là nhóm ![]() và tứ phân vị thứ ba là:
và tứ phân vị thứ ba là:

Khoảng biến thiên của mẫu số liệu ghép nhóm là:
Vì ![]() nên mức thu nhập của người lao động nhà máy B biến động nhiều hơn.
nên mức thu nhập của người lao động nhà máy B biến động nhiều hơn.
Giải rút gọn bài 3.3 trang 79 sách toán 12 tập 1 kntt
Bảng sau đây cho biết chiều cao của các học sinh lớp 12A và 12B.
| Chiều cao (cm) | ||||||
| Số học sinh của lớp 12A | 1 | 0 | 15 | 12 | 10 | 5 |
| Số học sinh của lớp 12B | 0 | 0 | 17 | 10 | 9 | 6 |
- Tìm khoảng biến thiên, khoảng tứ phân vị cho các mẫu số liệu ghép nhóm về chiều cao của học sinh lớp 12A, 12B.
- Để so sánh độ phân tán về chiều cao của học sinh hai lớp này ta nên dùng khoảng biến thiên hay khoảng tứ phân vị? Vì sao?
Giải rút gọn:
a) Lớp 12A: Khoảng biến thiên:![]()
Ta có cỡ mẫu![]() . Gọi
. Gọi ![]() là chiều cao của các học sinh lớp 12A và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
là chiều cao của các học sinh lớp 12A và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ nhất là nhóm
nên nhóm chứa tứ phân vị thứ nhất là nhóm ![]() và tứ phân vị thứ nhất là:
và tứ phân vị thứ nhất là: 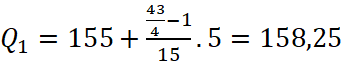 .
.
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ ba là nhóm
nên nhóm chứa tứ phân vị thứ ba là nhóm ![]() và tứ phân vị thứ ba là:
và tứ phân vị thứ ba là:
 .
.
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
![]()
Lớp 12B: Khoảng biến thiên:![]()
Ta có cỡ mẫu![]() . Gọi
. Gọi ![]() là là chiều cao của các học sinh lớp 12B và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
là là chiều cao của các học sinh lớp 12B và giả sử dãy số liệu gốc này đã được sắp xếp theo thứ tự không giảm.
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ nhất là nhóm
nên nhóm chứa tứ phân vị thứ nhất là nhóm ![]() và tứ phân vị thứ nhất là:
và tứ phân vị thứ nhất là:  .
.
Vì  và
và ![]() nên nhóm chứa tứ phân vị thứ ba là nhóm
nên nhóm chứa tứ phân vị thứ ba là nhóm ![]() và tứ phân vị thứ ba là:
và tứ phân vị thứ ba là:
 .
.
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: 
b) Ta nên dùng khoảng tứ phân vị vì khoảng tứ phân vị chỉ phụ thuộc vào nửa giữa của mẫu số liệu, không bị ảnh hưởng bởi các giá trị bất thường.
