Slide bài giảng Toán 12 kết nối Bài tập cuối chương I
Slide điện tử Bài tập cuối chương I. Kiến thức bài học được hình ảnh hóa, sinh động hóa. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 12 Kết nối tri thức sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI TẬP CUỐI CHƯƠNG I
A. TRẮC NGHIỆM
Giải rút gọn bài 1.30 trang 42 sách toán 12 tập 1 kntt
Cho hàm số ![]() có đạo hàm trên khoảng
có đạo hàm trên khoảng ![]() . Phát biểu nào dưới đây là đúng?
. Phát biểu nào dưới đây là đúng?
- Nếu
 với mọi
với mọi 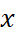 thuộc
thuộc  thì hàm số
thì hàm số  đồng biến trên
đồng biến trên 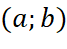 .
. - Nếu
 với mọi
với mọi  thuộc
thuộc 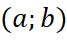 thì hàm số
thì hàm số  đồng biến trên
đồng biến trên 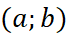 .
. - Hàm số
 đồng biến trên
đồng biến trên  khi và chỉ khi
khi và chỉ khi 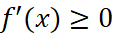 với mọi
với mọi  thuộc
thuộc 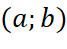 .
. - Hàm số
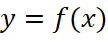 đồng biến trên
đồng biến trên  khi và chỉ khi
khi và chỉ khi  với mọi
với mọi 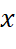 thuộc
thuộc 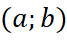 .
.
Giải rút gọn:
Chọn đáp án A.
Giải rút gọn bài 1.31 trang 42 sách toán 12 tập 1 kntt
Hàm số nào sau đây nghịch biến trên ℝ?
 .
.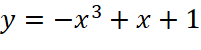 .
.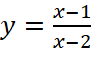 .
. .
.
Giải rút gọn:
Chọn đáp án A.
Giải rút gọn bài 1.32 trang 42 sách toán 12 tập 1 kntt
Hàm số nào dưới đây không có cực trị?
 .
.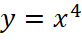 .
.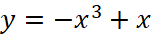
 .
.
Giải rút gọn:
Chọn đáp án D.
Giải rút gọn bài 1.33 trang 42 sách toán 12 tập 1 kntt
Giá trị cực tiểu của hàm số 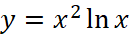 là:
là:
 .
. .
. .
.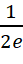 .
.
Giải rút gọn:
Chọn đáp án C.
Giải rút gọn bài 1.34 trang 42 sách toán 12 tập 1 kntt
Giá trị lớn nhất của hàm số 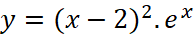 trên đoạn
trên đoạn ![]() là:
là:
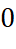 .
. .
.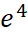 .
. .
.
Giải rút gọn:
Chọn đáp án B.
Giải rút gọn bài 1.35 trang 42 sách toán 12 tập 1 kntt
Cho hàm số ![]() thỏa mãn:
thỏa mãn:  ;
;  ;
; 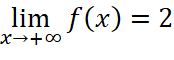 ;
; 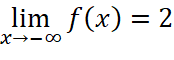 .
.
Khẳng định nào sau đây là đúng?
- Đường thẳng
 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số. - Đường thẳng
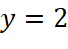 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số. - Đường thẳng
 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số. - Đường thẳng
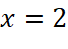 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Giải rút gọn:
Chọn đáp án B.
Giải rút gọn bài 1.36 trang 42 sách toán 12 tập 1 kntt
Tiệm cận xiên của đồ thị hàm số 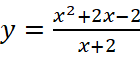 là:
là:
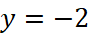 .
.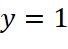 .
.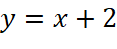 .
. .
.
Giải rút gọn:
Chọn đáp án D.
Giải rút gọn bài 1.37 trang 43 sách toán 12 tập 1 kntt
Cho hàm số ![]() xác định trên
xác định trên ![]() , liên tục trên mỗi khoản xác định và có bảng biến thiên như sau:
, liên tục trên mỗi khoản xác định và có bảng biến thiên như sau:

Khẳng định nào sau đây là sai?
- Đường thẳng
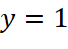 là tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận ngang của đồ thị hàm số đã cho. - Đường thẳng
 là tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận ngang của đồ thị hàm số đã cho. - Đường thẳng
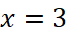 là tiệm cận đứng của đồ thị hàm số đã cho.
là tiệm cận đứng của đồ thị hàm số đã cho. - Đường thẳng
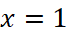 là tiệm cận đứng của đồ thị hàm số đã cho.
là tiệm cận đứng của đồ thị hàm số đã cho.
Giải rút gọn:
Chọn đáp án D.
Giải rút gọn bài 1.38 trang 43 sách toán 12 tập 1 kntt
Đồ thị trong Hình 1.37 là đồ thị của hàm số:
 .
.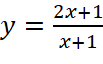 .
.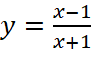 .
. .
.

Giải rút gọn:
Chọn đáp án B.
Giải rút gọn bài 1.39 trang 43 sách toán 12 tập 1 kntt
Đồ thị trong Hình 1.38 là đồ thị của hàm số:
 .
.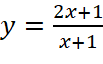
 .
.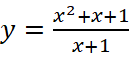 .
.

Giải rút gọn:
Chọn đáp án D.
B. TỰ LUẬN
Giải rút gọn bài 1.40 trang 43 sách toán 12 tập 1 kntt
Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:
 .
.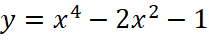
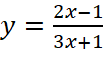 .
. .
.
Giải rút gọn:
-
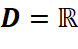 .
.
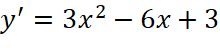 ;
;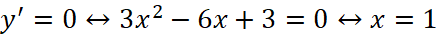
Bảng biến thiên:

Hàm số đồng biến trên các khoảng ![]() và
và ![]() .
.
Hàm số không có điểm cực trị.
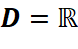 .
.
 ;
; 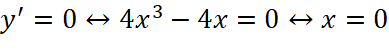 hoặc
hoặc![]()
Bảng biến thiên:
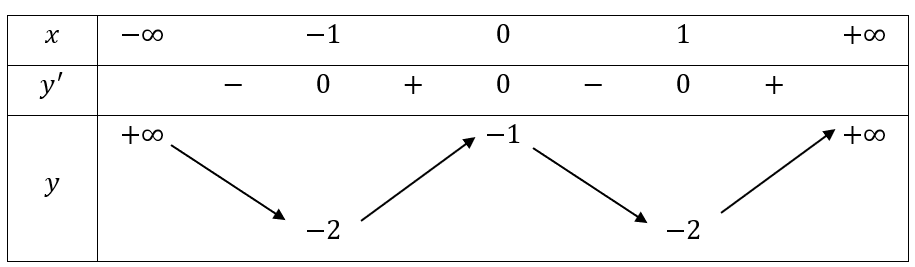
Hàm số đồng biến trên các khoảng ![]() và
và ![]() .
.
Hàm số nghịch biến trên các khoảng ![]() và
và ![]() .
.
Hàm số đạt cực đại tại ![]() và
và ![]() .
.
Hàm số đạt cực tiểu tại ![]() ;
; ![]() và
và ![]() .
.
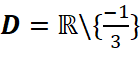 .
.
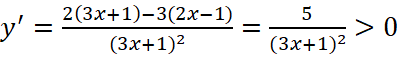 với
với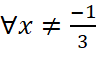
Hàm số đồng biến trên các khoảng  và
và 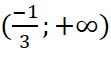 .
.
Hàm số không có cực trị.
 .
.
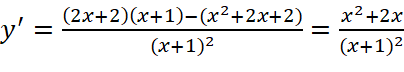 ;
;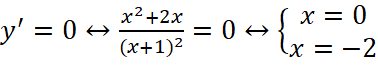
Bảng biến thiên:

Hàm số đồng biến trên các khoảng ![]() và
và ![]() .
.
Hàm số nghịch biến trên các khoảng ![]() và
và ![]() .
.
Hàm số đạt cực đại tại ![]() và
và ![]() .
.
Hàm số đạt cực tiểu tại ![]() và
và ![]() .
.
Giải rút gọn bài 1.41 trang 44 sách toán 12 tập 1 kntt
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
 trên nửa khoảng
trên nửa khoảng  ;
;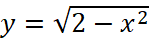 .
.
Giải rút gọn:
a) 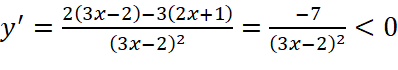 với
với![]()
Do đó  và hàm số không có giá trị nhỏ nhất trên nửa khoảng
và hàm số không có giá trị nhỏ nhất trên nửa khoảng ![]() .
.
b)  .
.
 ;
; ![]() (thỏa mãn)
(thỏa mãn)
 ;
;  ;
;
Vậy  ;
;
Giải rút gọn bài 1.42 trang 44 sách toán 12 tập 1 kntt
Tìm các tiệm cận của mỗi đồ thị hàm số sau:
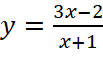 ;
;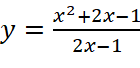 .
.
Giải rút gọn:
a) ![]() .
.
 ;
;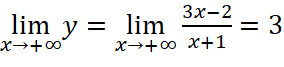
Vậy đồ thị hàm số có một tiệm cận ngang là ![]() .
.
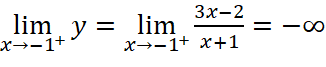 ;
;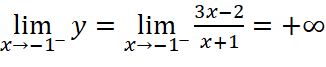
Vậy đồ thị hàm số có một tiệm cận đứng là ![]() .
.
b) 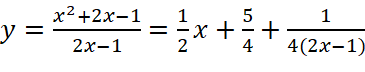
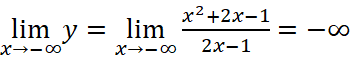 ;
;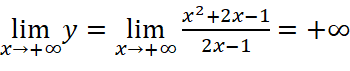
Vậy đồ thị hàm số không có tiệm cận ngang.
 ;
;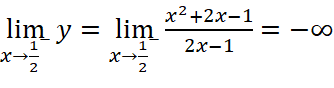
Vậy đồ thị hàm số có một tiệm cận đứng là  .
.
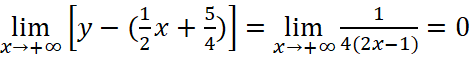
Vậy đồ thị hàm số có một tiệm cận xiên là  .
.
Giải rút gọn bài 1.43 trang 44 sách toán 12 tập 1 kntt
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) ;;
;;
b) 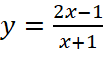 ;
;
c)  .
.
Giải rút gọn:
 .
.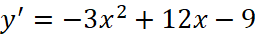 ;
;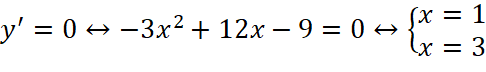
Trên khoảng ![]() ,
, ![]() nên hàm số đồng biến.
nên hàm số đồng biến.
Trên các khoảng ![]() và
và ![]() ,
, ![]() nên hàm số nghịch biến.
nên hàm số nghịch biến.
Hàm số đạt cực tiểu tại ![]() và
và ![]() .
.
Hàm số đạt cực đại tại ![]() và
và ![]() .
.
Giới hạn tại vô cực:
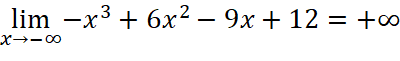 ;
;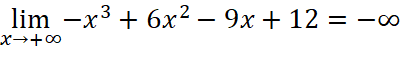
Bảng biến thiên:

- Đồ thị:

Giao điểm của đồ thị với trục ![]() là
là ![]() .
.
Đồ thị hàm số đi qua các điểm ![]() và
và ![]() .
.
Đồ thị hàm số có tâm đối xứng là ![]() .
.
 .
.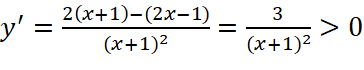 với
với
Hàm số đồng biến trên các khoảng ![]() và
và![]()
Hàm số không có cực trị.
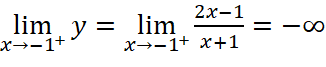 ;
;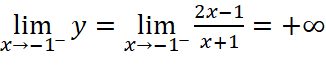
Vậy ![]() là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
 ;
;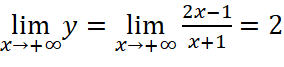
Vậy ![]() là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Bảng biến thiên:

- Đồ thị:

Giao điểm của đồ thị hàm số với trục ![]() là
là 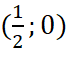 .
.
Giao điểm của đồ thị hàm số với trục ![]() là
là ![]() .
.
Đồ thị hàm số nhận giao điểm ![]() của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng.
của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng.
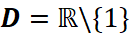 .
.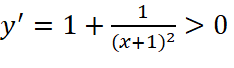 với
với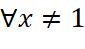
Hàm số đồng biến trên các khoảng ![]() và
và ![]() .
.
Hàm số không có cực trị.
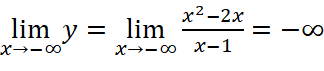 ;
;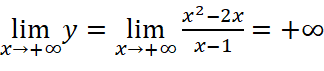
Vậy đồ thị hàm số không có tiệm cận ngang.
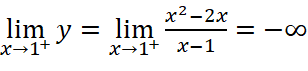 ;
;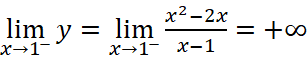
Vậy đồ thị hàm số có một tiệm cận đứng là ![]() .
.
 ;
;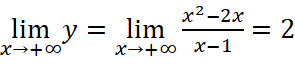
Vậy đồ thị hàm số có một tiệm cận xiên là ![]() .
.
Bảng biến thiên:
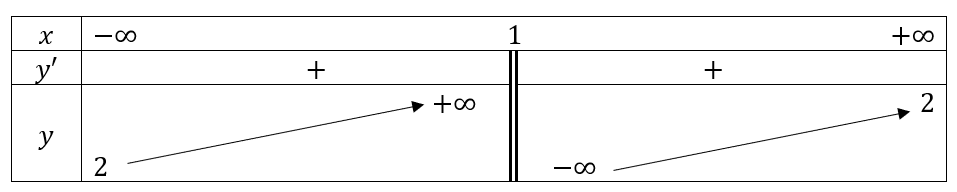
- Đồ thị:

Giao điểm của đồ thị hàm số với trục ![]() là
là ![]() và
và ![]() .
.
Giao điểm của đồ thị hàm số với trục ![]() là
là ![]() .
.
Đồ thị hàm số nhận giao điểm ![]() của hai đường tiệm cận làm tâm đối xứng và các đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng.
của hai đường tiệm cận làm tâm đối xứng và các đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng.
Giải rút gọn bài 1.44 trang 44 sách toán 12 tập 1 kntt
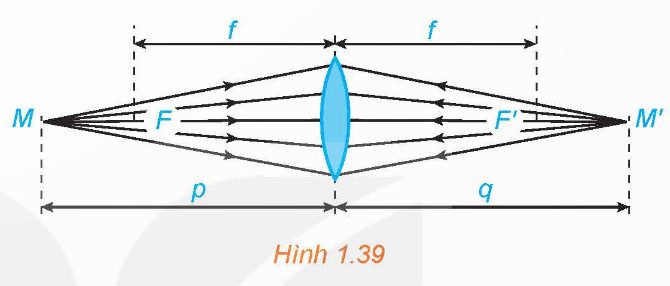
Xét một thấu kính hội tụ có tiêu cự ![]() (H.1.39). Khoảng cách
(H.1.39). Khoảng cách ![]() từ vật đến thấu kính liên hệ với khoảng cách
từ vật đến thấu kính liên hệ với khoảng cách ![]() từ ảnh đến thấu kính bởi hệ thức:
từ ảnh đến thấu kính bởi hệ thức:
 .
.
- Viết công thức tính
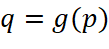 như một hàm số của biến
như một hàm số của biến  .
. - Tính các giới hạn
 ;
;  và giải thích ý nghĩa các kết quả này.
và giải thích ý nghĩa các kết quả này. - Lập bảng biến thiên của hàm số
 trên khoảng
trên khoảng 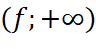 .
.
Giải rút gọn:
a) 
Do đó  với
với ![]() .
.
b) 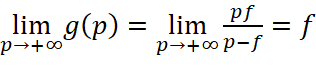 ;
;
Ý nghĩa là khoảng cách từ vật đến thấu kính tiến ra vô cùng thì khoảng cách từ ảnh đến thấu kính xấp xỉ tiêu cự.
là khoảng cách từ vật đến thấu kính tiến ra vô cùng thì khoảng cách từ ảnh đến thấu kính xấp xỉ tiêu cự.
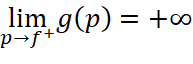 là khoảng cách từ vật đến thấu kính tiến gần về tiêu cự
là khoảng cách từ vật đến thấu kính tiến gần về tiêu cự ![]() thì khoảng cách từ ảnh đến thấu kính càng lớn.
thì khoảng cách từ ảnh đến thấu kính càng lớn.
c) 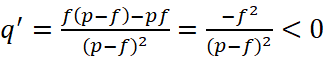 với
với![]()
Do đó hàm số![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() .
.
Giải rút gọn bài 1.45 trang 44 sách toán 12 tập 1 kntt
Dân số của một quốc gia sau ![]() (năm) kể từ năm 2023 được ước tính bởi công thức:
(năm) kể từ năm 2023 được ước tính bởi công thức:
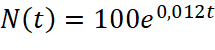 (
(![]() được tính bằng triệu người,
được tính bằng triệu người, ![]() ).
).
- Ước tính dân số của quốc gia này vào các năm 2030 và 2035 (kết quả tính bằng triệu người, làm tròn kết quả đến chữ số thập phân thứ ba).
- Xem
 là hàm số của biến số
là hàm số của biến số 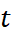 xác định trên đoạn
xác định trên đoạn  . Xét chiều biến thiên của hàm số
. Xét chiều biến thiên của hàm số 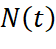 trên đoạn
trên đoạn 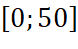 .
. - Đạo hàm của hàm số
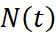 biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/năm). Vào năm nào tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/năm?
biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/năm). Vào năm nào tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/năm?
Giải rút gọn:
a) Dân số của quốc gia này vào các năm 2030 ![]() là:
là:
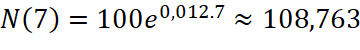 (triệu người)
(triệu người)
Dân số của quốc gia này vào các năm 2035 ![]() là:
là:
 (triệu người)
(triệu người)
b) 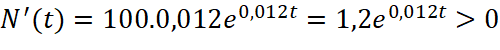 với
với![]()
Do đó hàm số ![]() luôn đồng biến trên đoạn
luôn đồng biến trên đoạn ![]() .
.
c) 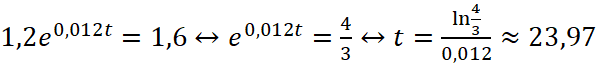 (năm)
(năm)
Vậy vào năm 2046 tốc độ tăng dân số của quốc gia đó là ![]() triệu người/năm.
triệu người/năm.
Giải rút gọn bài 1.46 trang 44 sách toán 12 tập 1 kntt
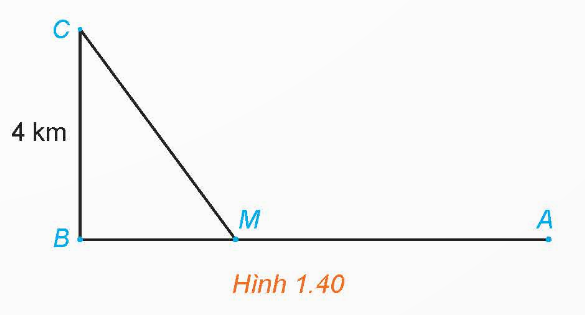
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như Hình 1.40. Khoảng cách từ C đến B là 4 km. Bờ biển chạy thẳng từ A đến B với khoảng cách là 10 km. Tổng chi phí lắp đặt cho 1 km dây điện trên biển là 50 triệu đồng, còn trên đất liền là 30 triệu đồng. Xác định vị trí điểm M trên đoạn AB (điểm nối dây từ đất liền ra đảo) để tổng chi phí lắp đặt là nhỏ nhất.
Giải rút gọn:
Gọi khoảng cách ![]() là
là ![]() (km).
(km).![]()
Khi đó khoảng cách![]() là:
là: ![]() (km)
(km)
Khoảng cách ![]() là:
là:  (km)
(km)
Khi đó chi phí lắp đặt dây điện là: 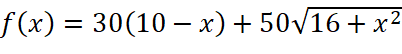 (triệu đồng)
(triệu đồng)
Ta có: 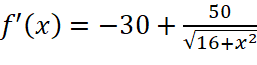 ;
;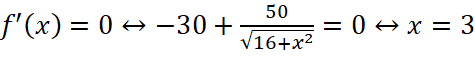
Ta có: ![]() ;
; ![]() ;
;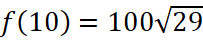
Do đó chi phí nhỏ nhất để lắp dây điện là ![]() triệu đồng khi
triệu đồng khi ![]() cách
cách ![]() một đoạn 3 km trên đoạn
một đoạn 3 km trên đoạn ![]() .
.
