Bài giảng điện tử chuyên đề Toán 11 cánh diều

CHÀO MỪNG CẢ LỚP ĐẾN VỚI TIẾT HỌC HÔM NAY! 

KHỞI ĐỘNG 

Tranh Đông Hồ là một dòng tranh dân gian Việt Nam, xuất xứ từ làng Đông Hồ (xã Song Hồ, huyện Thuận Thành, tỉnh Bắc Ninh). Tranh được in trên giấy điệp, màu sắc được sử dụng là màu tự nhiên: màu đen từ than lá tre, màu xanh từ lá chàm, màu đỏ từ sỏi,... Nghề làm tranh dân gian Đông Hồ là di sản văn hóa phi vật thể cấp Quốc gia. 

Ba bức tranh trong Hình 46 có hình dạng giống hệt nhau nhưng có kích thước to nhỏ khác nhau gợi nên những hình có mối liên hệ gì? 

CHUYÊN ĐỀ I. PHÉP BIẾN HÌNH PHẲNG 

BÀI 2. PHÉP ĐỒNG DẠNG 

NỘI DUNG BÀI HỌC 

Phép đồng dạng phối cảnh (phép vị tự) 

Phép đồng dạng 

1. PHÉP ĐỒNG DẠNG PHỐI CẢNH (PHÉP VỊ TỰ)
2. Khái niệm

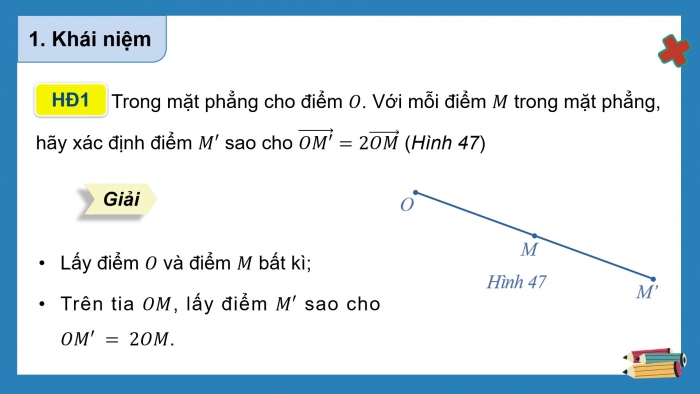
HĐ 1: Trong mặt phẳng cho điểm O. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M′ sao cho (OM′) ⃗=2(OM) ⃗ (Hình 47) 

Giải 

Lấy điểm O và điểm M bất kì; 

Trên tia OM, lấy điểm M′ sao cho OM′ = 2OM. 

KẾT LUẬN 

Cho điểm O cố định và số thực k không đổi, k≠0. Phép biến hình biến mỗi điểm M thành điểm M′ sao cho (OM′) ⃗=k(OM) ⃗ được gọi là phép vị tự tâm O tỉ số k, kí hiệu V_(O;k). 

Điểm M^′ được gọi là ảnh của điểm M, kí hiệu M^′=V_(O;k)(M). 

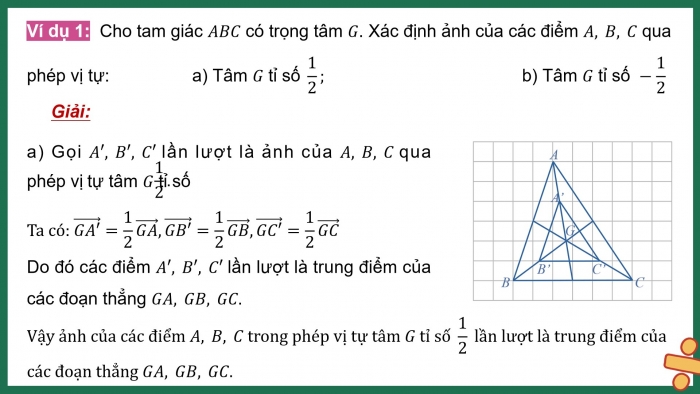
Ví dụ 1:  Cho tam giác ABC có trọng tâm G. Xác định ảnh của các điểm A, B, C qua  

phép vị tự:                 a) Tâm G tỉ số 1/2;                                        b) Tâm G tỉ số −1/2 

Giải: 

1. a) Gọi A′, B′, C′ lần lượt là ảnh của A, B, C qua phép vị tự tâm G tỉ số

Ta có: (GA′) ⃗=1/2(GA) ⃗,(GB′) ⃗=1/2(GB) ⃗,(GC′) ⃗=1/2(GC) ⃗ 

Do đó các điểm A′, B′, C′ lần lượt là trung điểm của các đoạn thẳng GA, GB, GC. 

Vậy ảnh của các điểm A, B, C trong phép vị tự tâm G tỉ số 1/2 lần lượt là trung điểm của các đoạn thẳng GA, GB, GC. 

1. b) Gọi D, E, F lần lượt là trung điểm của các cạnh  BC, CA, AB. Theo tính chất trọng tâm ta có:

(GD) ⃗=−1/2(GA) ⃗,(GE) ⃗=−1/2(GB) ⃗,(GF) ⃗=−1/2(GC) ⃗ 

Vậy ảnh của các điểm A, B, C qua phép vị tự tâm  

G tỉ số −1/2 lần lượt là các điểm D, E, F. 

Luyện tập 1 

Cho tam giác ABC có O là trung điểm của cạnh BC. Xác định ảnh của tam giác ABC trong phép vị tự tâm O tỉ số k=1/2 

Giải 

Gọi A^′, B^′, C^′ lần lượt là ảnh của A, B, C qua phép  

vị tự tâm O tỉ số k=1/2.Khi đó ta có: 

(OA^′) ⃗=1/2(OA) ⃗; (OB^′) ⃗=1/2(OB) ⃗;(OC^′) ⃗=1/2(OC) ⃗ 

Do đó, các điểm A^′, B^′, C^′ lần lượt là trung điểm của OA, OB, OC. 

2. Tính chất

HĐ 2: Cho phép vị tự tâm O tỉ số k và hai điểm A, B.  

Giả sử A′ = V_(O, k)(A), B′ = V_(O, k)(B) 

1. a) Biểu diễn các vectơ (OA′) ⃗,(OB′) ⃗ lần lượt theo các vectơ (OA) ⃗, (OB) ⃗.
2. b) Biểu diễn các vectơ (A′B′) ⃗ theo vectơ (AB) ⃗. Từ đó, tìm mối liên hệ độ dài giữa hai đoạn thẳng A′B′ và AB.

Giải: 

1. a) Vì A′ = V_(O, k)(A), B′ = V_(O, k)(B) nên (OA′) ⃗=k(OA) ⃗,  (OB′) ⃗=k(OB) ⃗
2. b) (A′B′) ⃗=(OB′) ⃗−(OA^′) ⃗=k(OB) ⃗−k(OA) ⃗=k((OB) ⃗−(OA) ⃗)=k(AB) ⃗

⇒(A′B′) ⃗=k(AB) ⃗⇒A^′B^′=|k|AB 

ĐỊNH LÍ 

Nếu phép vị tự tâm O tỉ số k (k≠0) lần lượt biến hai điểm A, B thành hai điểm A′, B′ thì (A′B′) ⃗=k(AB) ⃗ và A^′B^′=|k|AB. 

HĐ 3: Cho phép vị tự tâm O tỉ số k và ba điểm A, B,C sao cho B nằm giữa A và C. Giả sử A^′= V_(O, k)(A), B^′= V_(O, k)(B),C^′= V_(O, k)(C). 

1. a) Biểu diễn các vectơ (B′A′) ⃗,(B^′C′) ⃗ lần lượt theo các vectơ (BA) ⃗, (BC) ⃗.
2. b) Hai vectơ (BA) ⃗ và (BC) ⃗ có ngược hướng không?
3. c) Hai vectơ (B′A′) ⃗ và (B′C′) ⃗ có ngược hướng không? Từ đó, nêu mối liên hệ giữa ba điểm A^′, B^′,C^′.

Giải: 

1. a) Vì A′ = V_(O, k)(A), B′ = V_(O, k)(B), C′ = V_(O, k)(C)

nên (B′A′) ⃗=k(BA) ⃗ và (B′C′) ⃗=k(BC) ⃗ 

1. b) Vì A, B, C thẳng hàng và B nằm giữa A và C nên hai vectơ (BA) ⃗  và (BC) ⃗ ngược hướng với nhau.
2. c) Với k>0, ta có:

(B′A′) ⃗=k(BA) ⃗, nên hai vectơ (B′A′) ⃗;(BA) ⃗  cùng hướng với nhau. 

(B′C′) ⃗=k(BC) ⃗, nên hai vectơ (B′C′) ⃗; (BC) ⃗  cùng hướng với nhau. 

Mà hai vectơ (BA) ⃗; (BC) ⃗ ngược hướng với nhau nên (B′A′) ⃗;(B′C′) ⃗ ngược hướng nhau. 

Với k<0, tương tự.  

Vậy (B′A′) ⃗;(B′C′) ⃗ ngược hướng nhau. 

ĐỊNH NGHĨA 

Phép vị tự biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự của ba điểm đó. 

Hệ quả 

Phép vị tự tỉ số k(k≠0): 

• Biến đường thẳng thành đường thẳng song song hoặc trùng với nó; 
• Biến tia thành tia; 
• Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với |k|; 
• Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là |k|; 
• Biến góc thành góc bằng nó; 
• Biến đường tròn có bán kính R thành đường tròn có bán kính      R^′=|k|R và có tâm là ảnh của tâm. 

Chú ý 

Qua phép vị tự tâm O tỉ số k, ảnh của một đường thẳng trùng với chính nó khi và chỉ khi k = 1 hoặc O thuộc đường thẳng. 

Ví dụ 2: Cho tam giác ABC nhọn, không cân, nội tiếp đường tròn (O). Gọi G, H lần lượt là trọng tâm, trực tâm của tam giác ABC. Gọi D, E lần lượt là trung điểm của các cạnh BC, CA (Hình 50). Chứng minh rằng: 

1. a) Phép vị tự tâm G tỉ số−1/2 biến đường thẳng AH thành đường thẳng OD;
2. b) Phép vị tự tâm G tỉ số−1/2 biến điểm H thành điểm O;
3. c) Các điểm H, O, G thẳng hàng và   HG=2GO.

Giải 

1. a) Theo tính chất trọng tâm, ta có: (GD) ⃗=−1/2(GA) ⃗

Do đó, phép vị tự tâm G tỉ số −1/2  biến điểm  A  

thành điểm D.  

Suy ra, ảnh của đường thẳng AH qua phép      vị tự trên là một đường thẳng đi qua D và song song với AH. 

Mặt khác, ta có AH và OD vuông góc với BC nên AH song song với OD.  

Vậy phép vị tự tâm G tỉ số−1/2 biến đường thẳng AH thành đường thẳng OD. 

1. b)  Chứng minh tương tự câu a, ta có phép  vị tự tâm G tỉ số−1/2 biến đường thẳng BH thành đường thẳng OE.

Do đó, phép vị tự tâm G tỉ số −1/2  biến giao điểm H của AH và BH thành một điểm thuộc cả OD và OE là điểm O. 

1. c)  Vì phép vị tự tâm G tỉ số−1/2 biến điểm H

thành điểm O nên  (GO) ⃗=−1/2 (GH) ⃗. 

Suy ra các điểm H, G,O thẳng hàng và   HG=2GO. 

Ví dụ 3: Một thấu kính hội tụ có tiêu cự OF′=OF=5 cm (kính lúp). Vật sáng AB=4 cm được đặt vuông góc với trục chính của thấu kính, cách thấu kính một đoạn OA=3 cm, qua thấu kính cho ảnh ảo A′B′ (Hình 51). A′B′ là ảnh của AB qua phép vị tự tâm O tỉ số k. 

1. a) Tính khoảng cách AA′ từ vật đến ảnh theo đơn vị centimét.
2. b) Tính tỉ số k và độ cao của ảnh theo đơn vị centimét. Nhận xét kích thước của ảnh qua thấu kính hội tụ trên.

Giải 

1. a) Áp dụng định lí Thales, ta có:

A^′A/A^′O=B^′B/B^′O=BH/OF′=OA/OF=3/5 

Mà A′O−A′A=OA=3 (cm) 

Suy ra 5/3A′A−A′A=OA=3  

hay A’A =4,5 (cm) 

Vậy khoảng cách từ vật đến ảnh là 4,5 cm. 

1. b) Vì A′B′ là ảnh của AB qua phép vị tự V_(O,k) nên

k=OA^′/OA=OA + AA^′/OA=3 + 4,5/3=2,5 

Do đó, A^′B^′=k|AB=2,5 .4=10 (cm) 

Ta thấy 10 >4 nên ảnh có kích thước lớn hơn vật. 

Ví dụ 4: Cho đường tròn (C) có tâm O bán kính R. Xác định ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số k = – 2. 

Giải 

...