Giải câu 4 trang 114 toán VNEN 9 tập 2

01 Đề bài:

Câu 4: Trang 114 toán VNEN 9 tập 2

Chứng minh rằng: Trong một tứ giác nội tiếp, góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó. Ngược lại, tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó là tứ giác nội tiếp.

Hướng dẫn: Xem hình 102

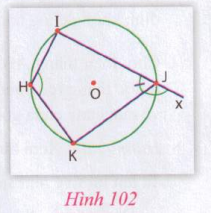
Nếu HIJK là tứ giác nội tiếp thì $\widehat{IHK} + \widehat{IJK} = 180^\circ$.

Mặt khác, $\widehat{IJK}$ và $\widehat{KJx}$ là hai góc kề bù, nên $\widehat{IJK} + \widehat{KJx} = 180^\circ$. Từ đó suy ra $....$

Ngược lại, nếu $\widehat{IHK} = \widehat{KJx}$ thì $\widehat{IHK} + \widehat{IJK} = \widehat{IJK} + \widehat{KJx} = 180^\circ$

Từ đó suy ra HIJK $.........$

02 Bài giải: