Giải câu 3 bài 3: Cấp số cộng
Câu 3: trang 97 sgk toán đại số và giải tích 11
Trong các bài toán về cấp số cộng, ta thường gặp năm đại lượng \(u_1, n, d, u_n, S_n\).
a) Hãy viết các hệ thức liên hệ giữa các đại lượng để có thể tìm được các đại lượng còn lại?
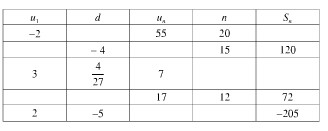
b) Lập bảng theo mẫu sau và điền vào chỗ trống thích hợp:
a)Ta có thể sử dụng các công thức sau:
$u_{n}=u_{1}+(n-1)d; d\geq 2$
$S_{n}=\frac{n(u_{1}+u_{n})}{2}$
$\Leftrightarrow S_{n}=n.u_{1}+\frac{n(n-1)}{2}d$
Cần biết ít nhất ba trong năm đại lượng \(u_1, n, d, u_n, S_n\) thì có thể tính được hai đại lượng còn lại.
b) Thực chất đây là năm bài tập nhỏ, mỗi bài ứng với các dữ liệu ở một dòng.
Ta giải từng bài tập nhỏ ta sẽ hoàn thành bảng.
- Biết \(u_1= -2, u_n= 55, n = 20\). Tìm \(d, S_n\)
Áp dụng công thức \(d = {{{u_n} - {u_1}} \over {n - 1}}=\frac{55-(-2)}{20-1}=3\)
\({S_n} = {{({u_1} + {u_n}).n} \over 2}=\frac{(-2+55).20}{2}=530\)
Đáp số: \(d = 3, S_{20}= 530\).
- Biết \(d = -4, n = 15\), \(S_n= 120\)
Tìm \(u_1,u_n\)
Áp dụng công thức \(u_{15}= u_1+ (n - 1)d=u_{1}+(15-1).(-4)=u_{1}-56\)
$\Leftrightarrow u_{1}-u_{15}=56$(1)
\({S_n} = {{({u_1} + {u_n}).n} \over 2}\)
$\Rightarrow S_{15} = {{({u_1} + {u_15}).15} \over 2}$
$\Leftrightarrow \frac{({u_1} + u_{15}).15}{2}=120$
$\Leftrightarrow ({u_1} + u_{15}).15=240$
$\Leftrightarrow {u_1} + u_{15}=16$(2)
Từ (1) và (2) ta có hệ sau:
\(\left\{ \matrix{{u_1} - {u_{15}} = 56 \hfill \cr {u_1} + {u_{15}} = 16 \hfill \cr} \right.\)
Giải hệ trên, ta được \(u_1= 36, u_{15}= - 20\).
- Áp dụng công thức \(u_n= u_1+ (n - 1)d\)
Ta có $n-1=\frac{u_{n}-u_{1}}{d}=\frac{7-3}{\frac{4}{27}}=27\Rightarrow n=28$
Áp dụng công thức \({S_n} = \frac{(u_{1}+u_{n}).n}{2}=\frac{(3+7).28}{2}=140$
Đáp số: \(n = 28\), \(S_n= 140\).
- Áp dụng công thức \({S_n} = {{({u_1} + {u_n}).n} \over 2}\)
$\Leftrightarrow u_{1}+u_{n}=\frac{S_{n}.2}{n}=\frac{72.2}{12}=12$
$\Rightarrow u_{1}=12-u_{n}=12-17=-5$
Áp dụng công thức
\(u_n= u_1+ (n - 1)d\Rightarrow d=\frac{u_{n}-u_{1}}{n-1}=\frac{17-(-5)}{12-1}=2\)
Đáp số: \(u_1= -5, d= 2\).
- Áp dụng công thức \({S_n} = {{\left[ {2{u_1} + (n - 1)d} \right].n} \over 2}\)
Thay số vào ta tìm được giá trị của n.
Tiếp theo áp dụng công thức \(u_n= u_1+ (n - 1)d\)
Ta tìm được giá trị của $u_{n}$
Đáp số: \(n = 10, u_n= -43\).
Ta được bảng sau:

Xem toàn bộ: Giải bài 3: Cấp số cộng
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 11 KNTT
Giải sgk lớp 11 CTST
Giải sgk lớp 11 cánh diều
Giải SBT lớp 11 kết nối tri thức
Giải SBT lớp 11 chân trời sáng tạo
Giải SBT lớp 11 cánh diều
Giải chuyên đề học tập lớp 11 kết nối tri thức
Giải chuyên đề toán 11 kết nối tri thức
Giải chuyên đề ngữ văn 11 kết nối tri thức
Giải chuyên đề vật lí 11 kết nối tri thức
Giải chuyên đề hóa học 11 kết nối tri thức
Giải chuyên đề sinh học 11 kết nối tri thức
Giải chuyên đề kinh tế pháp luật 11 kết nối tri thức
Giải chuyên đề lịch sử 11 kết nối tri thức
Giải chuyên đề địa lí 11 kết nối tri thức
Giải chuyên đề mĩ thuật 11 kết nối tri thức
Giải chuyên đề âm nhạc 11 kết nối tri thức
Giải chuyên đề công nghệ chăn nuôi 11 kết nối tri thức
Giải chuyên đề công nghệ cơ khí 11 kết nối tri thức
Giải chuyên đề tin học 11 định hướng Khoa học máy tính kết nối tri thức
Giải chuyên đề tin học 11 định hướng Tin học ứng dụng kết nối tri thức
Giải chuyên đề quốc phòng an ninh 11 kết nối tri thức
Giải chuyên đề hoạt động trải nghiệm hướng nghiệp 11 kết nối tri thức
Giải chuyên đề học tập lớp 11 chân trời sáng tạo
Giải chuyên đề học tập lớp 11 cánh diều
Trắc nghiệm 11 Kết nối tri thức
Trắc nghiệm 11 Chân trời sáng tạo
Trắc nghiệm 11 Cánh diều
Bộ đề thi, đề kiểm tra lớp 11 kết nối tri thức
Đề thi Toán 11 Kết nối tri thức
Đề thi ngữ văn 11 Kết nối tri thức
Đề thi vật lí 11 Kết nối tri thức
Đề thi sinh học 11 Kết nối tri thức
Đề thi hóa học 11 Kết nối tri thức
Đề thi lịch sử 11 Kết nối tri thức
Đề thi địa lí 11 Kết nối tri thức
Đề thi kinh tế pháp luật 11 Kết nối tri thức
Đề thi công nghệ cơ khí 11 Kết nối tri thức
Đề thi công nghệ chăn nuôi 11 Kết nối tri thức
Đề thi tin học ứng dụng 11 Kết nối tri thức
Đề thi khoa học máy tính 11 Kết nối tri thức
Bộ đề thi, đề kiểm tra lớp 11 chân trời sáng tạo
Bộ đề thi, đề kiểm tra lớp 11 cánh diều
Đề thi Toán 11 Cánh diều
Đề thi ngữ văn 11 Cánh diều
Đề thi vật lí 11 Cánh diều
Đề thi sinh học 11 Cánh diều
Đề thi hóa học 11 Cánh diều
Đề thi lịch sử 11 Cánh diều
Đề thi địa lí 11 Cánh diều
Đề thi kinh tế pháp luật 11 Cánh diều
Đề thi công nghệ cơ khí 11 Cánh diều
Đề thi công nghệ chăn nuôi 11 Cánh diều
Đề thi tin học ứng dụng 11 Cánh diều
Đề thi khoa học máy tính 11 Cánh diều

Bình luận