Giải bài tập 7 trang 68 SBT toán 7 tập 2 cánh diều
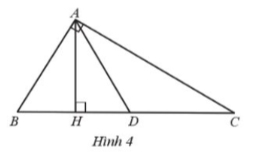
Bài 7. Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H, AD là tia phân giác của $\widehat{HAC}$ (Hình 4).
a) Tìm các cặp góc có tổng số đo bằng $90^{\circ}$
b) Cho $\widehat{C}=40^{\circ}$. Tính số đo của $\widehat{B}, \widehat{BDA}, \widehat{DAC}$.
c) Chứng minh: $\widehat{BAH}=\widehat{C};\widehat{CAH}=\widehat{B};\widehat{BAD}=\widehat{BDA}$
a) Các cặp góc có tổng số đo bằng $90^{\circ}$ là: $\widehat{BAH}$ và $\widehat{CAH}; \widehat{B}$ và $\widehat{C};\widehat{B}$ và $\widehat{BAH}; \widehat{C}$ và $\widehat{CAH};\widehat{BAD}$ và $\widehat{DAC};\widehat{HAD}$ và $\widehat{ADH}$.
b) Tam giác ABC vuông tại A nên $\widehat{B}=90^{\circ}-\widehat{C}=90^{\circ}-40^{\circ}=50^{\circ}$
Suy ra $\widehat{CAH}=90^{\circ}-\widehat{C}=50^{\circ}; \widehat{DAC}=\widehat{DAH}=50^{\circ}:2=25^{\circ}$
Do đó $\widehat{DAC}=25^{\circ}; \widehat{BDA}=90^{\circ}-\widehat{DAH}=65^{\circ}$
c) $\widehat{C}=\widehat{BAH}(=90^{\circ}-\widehat{B})$ và $\widehat{B}=\widehat{CAH}(=90^{\circ}-\widehat{C})$
Ta có $\widehat{DAC}+\widehat{BAD}=\widehat{BAC}=90^{\circ};\widehat{DAH}+\widehat{HDA}=90^{\circ}$
Mà $\widehat{DAC}=\widehat{DAH}$ suy ra $\widehat{BAD}=\widehat{BDA}$
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 7 cánh diều
Giải SBT lớp 7 kết nối tri thức
Giải SBT lớp 7 chân trời sáng tạo
Giải SBT lớp 7 cánh diều
Trắc nghiệm 7 Kết nối tri thức
Trắc nghiệm 7 Chân trời sáng tạo
Trắc nghiệm 7 Cánh diêu
Bình luận