Giải bài tập 4.12 trang 52 SBT toán 8 tập 1 kết nối:

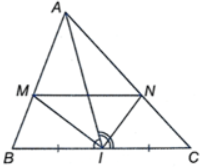
Trong ∆AIB, IM là phân giác của $\widehat{AIB}$ nên $\frac{MA}{MB}=\frac{IA}{IB}$ (tính chất đường phân giác của tam giác) (1)

Trong DAIC, IN là phân giác của $\widehat{AIC}$ nên $\frac{NA}{NC}=\frac{IA}{IC}$ (tính chất đường phân giác của tam giác) (2)

AI là đường trung tuyến của ∆ABC nên I là trung điểm của BC, do đó IB = IC (3)

Từ (1), (2), (3) ta có: $\frac{MA}{MB}=\frac{NA}{NC}$ 

Suy ra MN // BC (định lí Thales đảo).