Giải bài tập 3.25 trang 42 SBT toán 8 tập 1 kết nối:

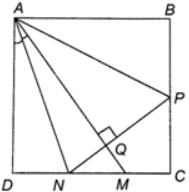
Đường thẳng NP ⊥ AM cắt AM ở Q.

Do ABCD là hình vuông nên ND ⊥ AD.

Xét ∆ADN vuông tại D và ∆AQN vuông tại Q có:

AN là cạnh chung, $\widehat{NAD}=\widehat{NAQ}$ (do AN là tia phân giác của )

Do đó ∆ADN = ∆AQN (cạnh huyền – góc nhọn)

Suy ra AD = AQ;

Mà AD = AB nên AQ = AB

Xét DAQP vuông tại Q và DABP vuông tại B có:

Cạnh AP chung; AQ = AB

Do đó ∆AQP = ∆ABP (cạnh huyền – cạnh góc vuông)

=> $\widehat{QAP}=\widehat{BAP}$

Ta có: $\widehat{BAD}=\widehat{DAN}+\widehat{NAQ}+\widehat{QAP}+\widehat{BAP}$

Mà $\widehat{NAD}=\widehat{NAQ}$ ; $\widehat{QAP}=\widehat{BAP}$

Nên ta có:

$\widehat{BAD}=2(\widehat{NAQ}+\widehat{PAQ})=\widehat{NAP}$

=> $\widehat{NAP}=\frac{1}{2}\widehat{DAB}=\frac{1}{2}.90^{o}$