Dạng bài tập về Các loại va chạm
Dạng 2: Các loại va chạm
Bài tập 1: Vật 1 khối lượng m đang chuyển động với tốc độ vo đến va chạm đàn hồi với vật 2 có cùng khối lượng và đang đứng yên. Nếu khối lượng vật 2 tăng lên gấp đôi thì động năng của hệ sau va chạm
Bài tập 2: Một ô tô con khối lượng 1,2 tấn đang chuyển động với tốc độ 25 m/s thì va chạm vào đuôi của một xe tải khối lượng 9 tấn đang chạy cùng chiều với tốc độ 20 m/s (Hình 19.4). Sau va chạm, ô tô con vẫn chuyển động theo hướng cũ với tốc độ 18 m/s.

a) Xác định vận tốc của xe tải ngay sau va chạm.
b) Xác định phần năng lượng tiêu hao trong quá trình va chạm. Giải thích tại sao lại có sự tiêu hao năng lượng này.
Bài tập 3: Con lắc đạn đạo là thiết bị được sử dụng để đo tốc độ của viên đạn. Viên đạn được bắn vào một khối gỗ lớn treo lơ lửng bằng dây nhẹ, không dãn. Sau khi va chạm, viên đạn ghim vào trong khối gỗ. Sau đó, toàn bộ hệ khối gỗ và viên đạn chuyển động như một con lắc lên độ cao h (Hình 19.3). Xét viên đạn có khối lượng m1 = 5 g, khối gỗ có khối lượng m2 = 1 kg và h = 5 cm. Lấy g = 9,8 m/s$^{2}$. Bỏ qua lực cản của không khí.
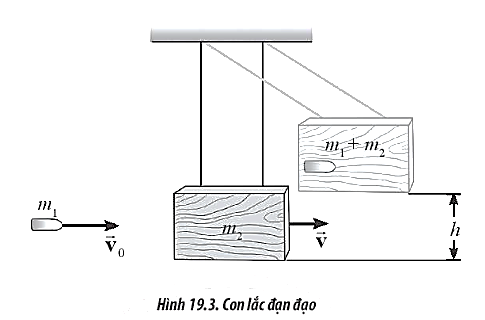
a) Tính vận tốc của hệ sau khi viên đạn ghim vào khối gỗ.
b) Tính tốc độ ban đầu của viên đạn.
Bài tập 1:
Vì va chạm là đàn hồi nên động năng của hệ sau va chạm bằng động năng của hệ trước va chạm và bằng động năng của vật 1 trước va chạm: $W_{đ}=\frac{1}{2}m.v_{o}^{2}$
Bài tập 2:
a) Gọi m1, m2 lần lượt là khối lượng xe ô tô con và xe tải; v1, v1’, v2, v2’ lần lượt là vận tốc của xe ô tô con, xe tải ngay trước và sau va chạm.
Áp dụng định luật bảo toàn động lượng cho hệ xe ô tô con xe tải ngay trước và sau khi xảy ra va chạm:
$m_{1}.\vec{v}_{1}+m_{2}.\vec{v}_{2}=m_{1}.\vec{v'}_{1}+m_{2}.\vec{v'}_{2}$(*)
Chiếu (*) lên hướng chuyển động ban đầu của ô tô con:
$m_{1}.v_{1}+m_{2}.v_{2}=m_{1}.v'_{1}+m_{2}.v'_{2}$
$\Rightarrow v'_{2}=\frac{m_{1}.v_{1}+m_{2}.v_{2}-m_{1}.v'_{1}}{m_{2}}=\frac{1200.25+9000.20-1200.18}{9000}\approx 20,93 m/s$
Như vậy, xe ô tô tải vẫn chuyển động theo hướng cũ với tốc độ 20,93 m/s.
b) Năng lượng tiêu hao trong quá trình va chạm:
$E=\frac{1}{2}m_{1}.v^{2}_{1}+\frac{1}{2}m_{2}.v^{2}_{2}-(\frac{1}{2}m_{1}.v'^{2}_{1}+\frac{1}{2}m_{2}.v'^{2}_{2})\approx 9308 J$
Năng lượng tiêu hao làm biến dạng kết cấu của hai xe, động năng các mảnh vỡ, nhiệt lượng ở bề mặt tiếp xúc, …
Bài tập 3:
a) Chọn gốc thế năng tại vị trí thấp nhất của con lắc
Áp dụng định luật bảo toàn cơ năng cho hệ ngay sau khi va chạm cho đến khi con lắc đạt độ cao cực đại:
$\frac{1}{2}(m_{1}+m_{2}).v^{2}=(m_{1}+m_{2}).g.h$
$\Rightarrow v=\sqrt{2.g.h}=\sqrt{2.9,8.0,05}\approx 0,99 m/s$.
b) Áp dụng định luật bảo toàn động lượng cho hệ khối gỗ - viên đạn ngay trước và sau va chạm:
$m_{1}.\vec{v}_{o}=(m_{1}+m_{2}).\vec{v}\Rightarrow\vec{v}_{o}=\frac{(m_{1}+m_{2}).\vec{v}}{m_{1}}$
Ta có độ lớn:
$v_{o}=\frac{(m_{1}+m_{2}).v}{m_{1}}=\frac{(0,005+1).0,99}{0,005}\approx198,99 m/s$

Bình luận