Dạng bài tập Chuyển động tròn và lực hướng tâm
Dạng 2: Chuyển động tròn và lực hướng tâm
Bài tập 1: Cho bán kính Trái Đất khoảng 6,37.10$^{6}$ m và gia tốc trọng trường ở gần bề mặt Trái Đất là 9,8 m/s$^{2}$. Một vệ tinh chuyển động tròn đều gần bề mặt Trái Đất phải có tốc độ bằng bao nhiêu để không rơi xuống mặt đất.
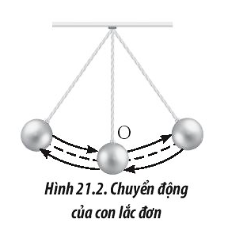
Bài tập 2: Một vật nặng có khối lượng bằng 5 kg được buộc vào một dây dài 0,8 m và thả cho chuyển động trong mặt phẳng thẳng đứng như Hình 21.2. Khi qua vị trí cân bằng O, vật có tốc độ 2,8 m/s. Tính gia tốc hướng tâm và lực căng dây khi vật đi qua vị trí cân bằng O. Lấy g = 9,8 m/s$^{2}$
Bài tập 3: Một chiếc xe đua có khối lượng 800 kg chạy với tốc độ lớn nhất (mà không bị trượt) theo đường tròn nằm ngang có bán kính 80 m (Hình 21.3) được một vòng sau khoảng thời gian 28,4 s. Tính:
a) gia tốc hướng tâm của xe.
b) hệ số ma sát nghỉ giữa các bánh xe và mặt đường. Lấy g = 9,8 m/s$^{2}$
Bài tập 1:
Trọng lực tác dụng lên vệ tinh đóng vai trò là lực hướng tâm:
$P=F_{ht}\Rightarrow m.g=m.\frac{v^{2}}{R}\Rightarrow v=\sqrt{g.R}=\sqrt{6,37.10^{6}.9,8}=7,9.10^{3} (m/s)$
Bài tập 2:
Tại VTCB O: $a_{ht}=\frac{v^{2}}{R}=\frac{v^{2}}{l}=\frac{2,8^{2}}{0,8}=9,8 m/s^{2}$
Hợp lực của trọng lực P và lực căng dây đóng vai trò là lực hướng tâm.
$\vec{F}_{ht}=\vec{P}+\vec{T}$
Chiếu biểu thức vectơ lên phương thẳng đứng của sợi dây, chiều dương hướng vào tâm quỹ đạo.
$F_{ht}=-P+T \Rightarrow T=F_{ht}+P$
$\Rightarrow T=m.a_{ht}+mg=m.(a_{ht}+g)=5.(9,8+9,8)=98 N$
Bài tập 3:
a) Tốc độ: $v=\omega.R=\frac{2\pi.R}{T}=\frac{2\pi.80}{28,4}\approx 39,2 m/s^{2}$
b) Vì tốc độ xe lớn nhất nên lực ma sát nghỉ (đóng vai trò là lực hướng tâm) có giá trị lớn nhất:
$F_{ms}=\mu.N=\mu. m.g=m.a_{ht} \Rightarrow \mu=\frac{a_{ht}}{g}=0,4$
Giải những bài tập khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận