1. NHÂN ĐƠN THỨC VỚI ĐA THỨC

• Quy tắc nhân đơn thức với đa thức

HĐ1:

- Để nhân hai đơn thức, ta nhân các hệ số với nhau và nhân các phần biến với nhau.

- Tính: 

   $(12x^{3}).(-5x^{2})$

$=[12.(-5)].(x^{3}.x^{2})$ 

$=-60x^{5}$

HĐ2: 

$2x.3x^{2}=6x^{3}$

$2x.(-8x)=-16x^{2}$

2x . 1 = 2x

=> Tổng các tích = $6x^{3}-16x^{2}+2x$

=> Kết luận:

Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.

Ví dụ 1 (SGK -tr36)

Luyện tập 1.  

$(-2x^{2}).(3x -4x^{3}+7 -x^{2})$

$= (-2x^{2}).3x+(-2x^{2}).(-4x^{3})+(-2x^{2}).7+(-2x^{2}).(-x^{2})$

$= -6x^{3}+8x^{5} -14x^{2}+2x^{4}$

$= 8x^{5}+2x^{4}-6x^{3} -14x^{2}$

Vận dụng 1:

a) $P(x)=7x^{2}(x^{2} -5x+2) -5x(x^{3} -7x^{2}+3x)$

$ =7x^{2}.x^{2}+7x^{2}.(-5x)+7x^{2}.2 -(5x.(x^{3})+5x.(-7x^{2})+5x.3x)$

$ =7x^{4} -35x^{3}+14x^{2} -5x^{4}+35x^{3} -15x^{2}$

$ =(7x^{4} -5x^{4})+(35x^{3} -35x^{3})+(-15x^{2} +14x^{2})$  

$ =2x^{4} -x^{2}$

b)  Thay x=- $\frac{1}{2}$ vào P(x), ta được:

$P(x)=2.(-\frac{1}{2})^{4}-(-\frac{1}{2})^{2}=-\frac{3}{8}$ 

Thử thách nhỏ

$x^{3}(x+2)-x(x^{3}+2^{3})-2x(x^{2}-2^{2})=x^{4}+2x^{3}-x^{4}-8x-2x^{3}+8x$

$=(x^{4}-x^{4})+(2x^{3}-2x^{3})+(-8x+8x) =0+0+0$

=0

2. NHÂN ĐA THỨC VỚI ĐA THỨC

• Nhân hai đa thức tuỳ ý

HĐ3: 

$2x.(x^{2} -5x+1)$

$=2x.x^{2}+2x.(-5x)+2x$

$=2x^{3} -10x^{2}+2x$

=> Kết luận:

Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.

Ví dụ 2: SGK -tr37

*Chú ý:

- Ta có thể trình bày phép nhân ở Ví dụ 2 bằng cách đặt tính nhân:

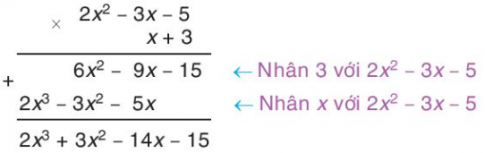
+ Khi nhân các hạng tử ở dòng dưới với đa thức ở dòng trên, ta nên nhân các hạng tử theo thứ tự từ bậc thấp đến bậc cao.

+  Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trong một dòng riêng.

+ Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau (để thực hiện phép cộng theo cột).

- Phép nhân đa thức cũng có các tính chất:

+ Giao hoán: A.B = B.A

+ Kết hợp: (A.B).C = A.(B.C)

+ Phân phối đối với phép cộng: 

A.(B + C) = A.B + A.C

Luyện tập 2: 

* Cách 1. Nhân từng hạng tử rồi cộng các tích với nhau.

$(x^{3} -2x^{2}+x -1)(3x -2)$

$=x^{3}.3x+x^{3}.(-2)+(-2x^{2}).3x+(-2x^{2}).(-2)+x.3x+x.(-2)+(-1).3x+(-1).(-2)$

$=3x^{4} -2x^{3} -6x^{3}+4x^{2}+3x^{2} -2x -3x+2$

$=3x^{4} -8x^{3}-7x^{2} -5x+2$

* Cách 2. Đặt tính nhân:

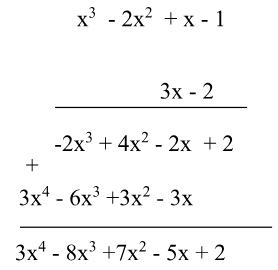
Vận dụng 2:

Gọi P = $(x-2)(2x^{3} -x^{2}+1)+(x -2)x^{2}(1 -2x)$.

C1: Ta có:

$P=(x -2)(2x^{3} -x^{2}+1)+(x -2)(x^{2}.1+x^{2}.(-2x))$

$=(x -2)(2x^{3} -x^{2}+1)+(x -2)(x^{2}-2x^{3})$

$=(x -2)(2x^{3} -x^{2}+1+x^{2}-2x^{3})$

=(x -2).1 

=(x -2) 

C2: Đặt $A =(x -2)(2x^{3} -x^{2}+1)$

$A = 2x^{4} -5x^{3} + 2x^{2} + x -2$

Đặt B = (x -2)x$^{2}$(1 -2x).

B = $-2x^{4} + 5x^{3} -2x^{2}$

P = A + B = x – 2.

Vận dụng 3:

a) Tính như sau:

- Kết quả thứ nhất: (x+1)$^{2}$

- Kết quả thứ hai: (x-1)$^{2}$

b) Đa thức biểu thị kết quả cuối: $(x+1)^{2} -(x-1)^{2} = 4x$

Vậy Pi chỉ việc chia kết quả cuối cùng cho 4 là ra tuổi của bạn.