I. CHIA ĐƠN THỨC CHO ĐƠN THỨC

HĐ1:

a) $x^{5} : x^{3}$ = $x^{5-3}$ = $x^{2}$

b) $(4x^{3}) : x^{2}$ = $4 . x^{3-2}$ = 4x

c) $\frac{a}{b} . x^{m-n}$

(a ≠ 0; b ≠ 0; m, n ∈ N; m ≥ n).

Kết luận: Muốn chia đơn thức A cho đơn thức B(B≠0) khi số mũ của biến trong A lớn hơn hoặc băng số mū của biến đó trong B, ta làm như sau:

• Chia hệ số của đơn thức A cho hệ số của đơn thức B;
• Chia luỹ thừa của biến trong A cho luỹ thừa của biến đó trong B;
• Nhân các kết quả vừa tìm được với nhau.

Chú ý: $(ax^{m}):(bx^{n})=\left ( \frac{a}{b} \right ).(x^{m}:x^{n})$

(a ≠ 0; b ≠ 0; m, n ∈ N; m ≥ n).

Ví dụ 1 (SGK- tr64)

LT1:

a) $(3x^{6}) : (0,5x^{4})$ = $(3 : 0.5) . (x^{6-4})$ = $6x^{2}$

b) $(-12x^{m+2}) : 4x^{n+2})$ = $(-12 : 4) . (x^{m+2-n+2})$ = $-3x^{m-n}$ 

II. CHIA ĐA THỨC CHO ĐƠN THỨC 

HĐ2:

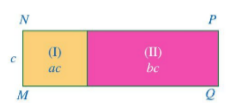
a) Độ dài cạnh kề với MN của hình chữ nhật (I) là A: c = ac : c = a.

Độ dài cạnh kề với PQ của hình chữ nhật (II) là B: c = bc : c = b.

Khi đó NP = a + b.

b) Diện tích MNPQ bằng tổng diện tích hai hình chữ nhật (I) và (II) bằng ac + bc.

Khi đó độ dài NP là thương trong phép chia diện tích hình chữ nhật MNPQ cho MN.

Hay NP = (ac + bc) : c = (A + B) : c.

Mà NP = a + b = A: c + B: c.

Do đó (A + B) : c = A : c + B : c.

Chú ý:

(A + B) : C = A : C = B : C

(A – B) : C = A : C – B : C

HĐ3:

$(4x^{2} + 3x) : (2x)$ = $(4x^{2}) : (2x) + (3x) : (2x)$ = $2x + \frac{3}{2}$

Kết luận: Muốn chia đa thức P cho đơn thức Q(Q ≠ 0) khi số mũ của biến ở mỗi đơn thức của P lớn hơn hoặc bằng số mũ của biến đó trong Q, ta chia mỗi đơn thức của đa thức P cho đơn thức Q rồi cộng các thương với nhau.

Ví dụ 2 (SGK- tr65)

LT2:

$\frac{1}{2}x^{4} - \frac{1}{4}x^{3} + x) : (\frac{-1}{8}x)$ = $(\frac{1}{2}x^{4} : \frac{-1}{8}x) - \frac{1}{4}x^{3} : (\frac{-1}{8}x)$ + $(x : \frac{-1}{8}x)$

= $-4x^{3} + 2x^{2} - 8$

III. CHIA ĐA THỨC MỘT BIẾN ĐÃ SẮP XẾP 

HĐ4:

a) $(2x^{2} + 5x + 2) : (2x + 1) = x + 2$

b) $(3x^{3} - 5x^{2} + 2) : (x^{2} + 1) = 3x -5$

Kết luận: Để chia một đa thức cho một đa thức khác đa thức không (cả hai đa thức đều đã thu gọn và sắp xếp các đơn thức theo số mũ giảm dần của biến) khi bậc của đa thức bị chia lớn hơn hoặc bằng bậc của đa thức chia, ta làm như sau:

Bước 1:

• Chia đơn thức bậc cao nhất của đa thừc bị chia cho đơn thức bậc cao nhất của đa thức chia
• Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột
• Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.

Bước 2: Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc nhỏ hơn bậc của đa thức chia.

Ví dụ 3 (SGK – tr66)

LT3:

a)

Vậy $(x^{3} + 1) : (x^{2} + x +1)$ = x + 1

b)

Vậy $(8x^{3} - 6x^{2} + 5) : (x^{2} + x + 1)$ = 8x + 14

Nhận xét:

Khi chia đa thức A cho đa thức B của cùng một biến (B ≠ 0), có hai khả năng xảy ra:

• Phép chia có dư bằng 0. Trong trường hợp này ta nói đa thức A chia hết cho đa thức B.
• Phép chia có dư là đa thức R (R ≠ 0) với bậc của R nhỏ hơn bậc của B. Phép chia trong trường hợp này được gọi là phép chia có dư.

Người ta chứng minh được rằng đối với hai đa thức tùy ý A và B của cùng một biến (B ≠ 0), tồn tại duy nhất một cặp đa thức Q và R sao cho A = B.Q+R, trong đó R bằng 0 hoặc bậc của R nhỏ hơn bậc của B. Như vậy, đa thức A chia hết cho đa thức B khi và chi khi R = 0.