CHƯƠNG III. HÀM SỐ BẬC HAI VÀ ĐỒ THỊ

BÀI 1. HÀM SỐ VÀ ĐỒ THỊ

1. KHÁI NIỆM HÀM SỐ

HĐKP1.  

a) Tập hợp các mốc giờ đã có dự báo nhiệt độ là:

A =  {1; 4; 7; 10; 13; 16; 19; 22}

b) Tập hợp các số đo nhiệt độ đã dự báo là:

B = {28; 27; 32; 31; 29; 28; 27}

c) Nhiệt  độ dự báo tại Thành phố Hồ Chí Minh vào lúc 7 giờ sáng ngày 01/5/2021 là: 28$^{\circ}$C. 

Kết luận:

Giả sử x và y là hai đại lượng biến thiên và x nhận giá trị thuộc tập số D.

Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập hợp số thực R thì ta có một hàm số.

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D gọi là tập xác định của hàm số.

Tập hợp T gồm tất cả các giá trị y (tương ứng với x thuộc D) gọi là  tập giá trị của hàm số.

* Nhận xét:

Một hàm số có thể được cho bằng bảng, bằng biểu đồ, hoặc bằng công thức.

Ví dụ 1:

a) Bảng dữ liệu dự báo thời tiết (Bảng 1) biểu thị một hàm số vì: ứng với mỗi thời điểm (giờ) trong bảng đều có một giá trị dự báo nhiệt độ duy nhất. 

Tập xác định của hàm số: 

D = {1; 4; 7; 10; 13; 16; 19; 22} và có tập giá trị T =  {27; 28; 29; 31; 32}

Tập giá trị của hàm số:

T = {27; 28;; 29; 31; 32}

b) Biểu đồ “ Dự báo nhiệt độ ngày 01/5/2021 tại Thành phố Hồ Chí Minh” biểu thị một hàm số vì: ứng với mỗi thời điểm (giờ) trong biểu đồ đều có một giá trị dự báo nhiệt độ duy nhất.

 TXĐ và tập giá trị của hàm số như câu a.

Chú ý:

a) Khi một hàm số được cho bằng công thức mà không chỉ rõ tập xác định thì ta quy ước:

Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

b) Một hàm số có thể được cho bởi hay hay nhiều công thức. Chẳng hạn, xét hàm số:

f(x)=$\left\{\begin{matrix}-2x +1 với x\leq 1 & \\ x^{2} với x > 1 & \end{matrix}\right.$

Nghĩa là với x$\leq $1 thì f(x)=-2x+1, với x > 1 thì f(x)=x$^{2}$

Ví dụ 2:

a) Biểu thức f(x) có nghĩa ⇔5-x≥0⇔x≤5

Vậy TXĐ của hàm số: D=(-∞5 ]

Vậy TXĐ của hàm số: D=R\{3}

Thực hành 1:

Bảng đó biểu thị một hàm số vì: 

Ứng với mỗi thời điểm t có duy nhất một giá trị v. 

Tập xác định của hàm số:

D = {0,5; 1; 1,2; 1,8; 2,5}.

Thực hành 2. 

a) f(x)=$\sqrt{2x+7}$

Biểu thức f(x) có nghĩa ⇔2x+7≥0⇔x≥$\frac{-7}{2}$

Vậy TXĐ của hàm số: D=[$\frac{-7}{2}$+ ∞)

b) f(x)=$\frac{x+4}{x^{2}-3x+2}$

Biểu thức f(x) có nghĩa x$^{2}$-3x+2≠0⇔(x-1)(x-2)≠0

⇔$\left\{\begin{matrix}x\neq 1 & \\ x\neq 2 & \end{matrix}\right.$ 

Vậy TXĐ của hàm số: D=R\{12 }

Vận dụng:

a) Công thức của hàm số biểu thị diện tích bồn hoa theo bán kính r là :

f(x)=$\frac{1}{4}$r$^{2}$

Tập xác định của hàm số : D=[0,53 ]

b) f(x)=0,5 π

$\frac{1}{4}$r$^{2}$=0,5 

r$^{2}$=2 

⇔r=±$\sqrt{2}$ (cm)

2. ĐỒ THỊ HÀM SỐ

HĐKP2.  

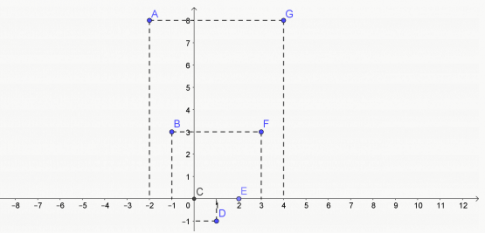
a) Tập xác định của hàm số là D = {-2; -1; 0; 1; 2; 3; 4}

b) 

Kết luận:

Cho hàm số y=f(x) có tập xác định D.

Trên mặt phẳng tọa độ Oxy, đồ thị (C) của hàm số là tập hợp tất cả các điểm M(x;y) với x ∈ D và y =f(x).

Vậy (C)= {M(x. F(x))| x $\in $ D}

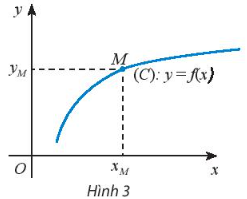
* Chú ý:

Điểm M(x$_{M}$ ; y$_{M}$) thuộc đồ thị hàm số y = f(x) khi và chỉ khi x$_{M} \in $ D và y$_{M}$ = f(x$_{M}$).

Ví dụ 3: SGK - tr44

Thực hành 3.

Với x = 0 => f(0) = 8. Ta có điểm A(0; 8)

Với x = $\frac{-8}{3}$=> f($\frac{-8}{3}$) = 0. Ta có điểm B($\frac{-8}{3}$; 0)

Vẽ đường thẳng f đi qua hai điểm A và B, ta có f là đồ thị của hàm số f(x) = 3x + 8.

3. HÀM SỐ ĐỒNG BIẾN, HÀM SỐ NGHỊCH BIẾN

HĐKP3: SGK -tr45 

 => Kết luận:

Với hàm số y = f(x) xác định trên khoảng (a ; b), ta nói:

Hàm số đồng biến trên khoảng (a ; b) nếu:

x$_{1}$, x$_{2} \in $ (a ; b), x$_{1}$< x$_{2}$ => f(x$_{1}$) < f(x$_{2}$).

Hàm số nghịch biến trên khoảng (a ; b) nếu:

x$_{1}$, x$_{2} \in $ (a ; b), x$_{1}$ < x$_{2}$ => f(x$_{1}$) > f(x$_{2}$).

* Nhận xét:

Khi hàm số đồng biến (tăng) trên khoảng (a ; b) thì đồ thị của nó có dạng đi lên từ trái sang phải. Ngược lại, khi hàm số nghịch biến (giảm) trên khoảng (a;b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.

Ví dụ 4: SGK - tr45

Ví dụ 5: SGK - tr46

Thực hành 4.

a) Từ đồ thị, ta thấy hàm số xác định trên [-3; 7]

Trên khoảng (-3; 1) và (3; 7), đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1) và (3;7).

Trên khoảng (1; 3), đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).

b) Xét hàm số y = f(x) = 5x$^{2}$ trên khoảng (2;5)

Lấy  tùy ý sao cho x$_{1}$ < x$_{2}$, ta có: 

f(x$_{1}$) - f(x$_{2}$) = 5(x$_{1}^{2}$ - x$_{2}^{2}$) = 5(x$_{1}$ + x$_{2}$)(x$_{1}$ - x$_{2}$) 

Do x$_{1}$ < x$_{2}$ nên x$_{1}$ - x$_{2}$ < 0 và do x$_{1}$, x$_{2} \in $ (2; 5) nên (x$_{1}$ + x$_{2}$) > 0. Từ đây suy ra f(x$_{1}$) - f(x$_{2}$) < 0 hay f(x$_{1}$) < f(x$_{2}$).

Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).