Giải Siêu nhanh Toán 12 Kết nối bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Giải Siêu nhanh bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số bộ sách Toán 12 kết nối tri thức tập 1. Phần đáp án ngắn gọn, hướng dẫn giải chi tiết cho từng bài tập có trong chương trình học của sách giáo khoa. Hi vọng, các em học sinh hiểu và nắm vững kiến thức môn Toán 12 kết nối tri thức chương trình mới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
1. SƠ ĐỒ KHẢO SÁT HÀM SỐ
Hoạt động 1: Làm quen với việc khảo sát và vẽ đồ thị hàm số.
Cho hàm số 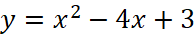 . Thực hiện lần lượt các yêu cầu sau:
. Thực hiện lần lượt các yêu cầu sau:
- Tính
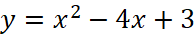 và tìm các điểm tại đó
và tìm các điểm tại đó 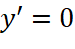 .
. - Xét dấu
 để tìm các khoảng đồng biến, khoảng nghịch biến và cực trị của hàm số.
để tìm các khoảng đồng biến, khoảng nghịch biến và cực trị của hàm số. - Tính
 ,
,  và lập bảng biến thiên của hàm số.
và lập bảng biến thiên của hàm số. - Vẽ đồ thị của hàm số và nhận xét về tính đối xứng của đồ thị.
Giải nhanh:
a. ![]() .
.
![]() ;
; ![]() (thỏa mãn)
(thỏa mãn)
Vậy ![]() tại
tại ![]() .
.
b. Trên khoảng ![]() ,
, ![]() nên hàm số nghịch biến. Trên khoảng
nên hàm số nghịch biến. Trên khoảng ![]() ,
, ![]() nên hàm số đồng biến.
nên hàm số đồng biến.
Hàm số đạt cực tiểu tại ![]() , giá trị cực tiểu
, giá trị cực tiểu ![]() . Hàm số không có cực đại.
. Hàm số không có cực đại.
c. 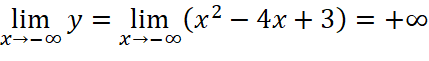
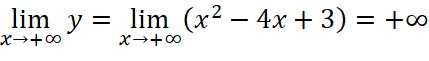

d.

Đồ thị giao với trục tung tại điểm có tọa độ là ![]() .
.
Ta có: 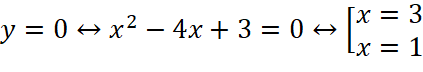 . Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm
. Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm ![]() và
và ![]() .
.
Xét điểm ![]() thuộc đồ thị hàm số, do đó đồ thị hàm số nhận đường thẳng
thuộc đồ thị hàm số, do đó đồ thị hàm số nhận đường thẳng ![]() làm trục đối xứng.
làm trục đối xứng.
2. KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ ĐA THỨC BẬC BA
Luyện tập 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số 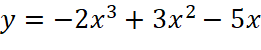 .
.
Giải nhanh:
![]() .
.
Sự biến thiên:
Ta có:  với
với ![]() .
.
=> Hàm số nghịch biến trên khoảng![]()
Hàm số không có cực trị.
Tiệm cận:  ;
;


Đồ thị:
Ta có: 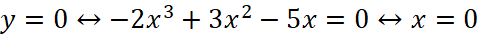 (thỏa mãn)
(thỏa mãn)
Vậy giao điểm của đồ thị hàm số với trục tung và trục hoành là điểm![]()
Tâm đối xứng là  .
.

3. KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ PHÂN THỨC HỮU TỈ
Luyện tập 2: Giải bài toán ở tình huống mở đầu, coi ![]() là hàm số xác định với
là hàm số xác định với ![]() .
.
Giải nhanh:

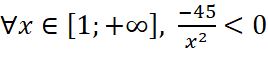 =>
=>  là hàm số giảm.
là hàm số giảm.

Vậy nên chi phí trung bình giảm theo ![]() nhưng luôn lớn hơn 2 triệu đồng/sản phẩm.
nhưng luôn lớn hơn 2 triệu đồng/sản phẩm.
Điều này thể hiện trên Hình 1.27 là đồ thị hàm số  có một tiệm cận ngang là đường thẳng
có một tiệm cận ngang là đường thẳng ![]() và đi xuống trong khoảng
và đi xuống trong khoảng ![]() .
.
Vận dụng: Một bể chứa ban đầu có 200 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 40 lít nước, đồng thời cho vào bể 20 gam chất khử trùng (hòa tan).
- Tính thể tích nước và khối lượng chất khử trùng có trong bể sau
 phút. Từ đó tính nồng độ chất khử trùng (gam/lít) trong bể sau
phút. Từ đó tính nồng độ chất khử trùng (gam/lít) trong bể sau 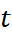 phút.
phút. - Coi nồng độ chất khử trùng là hàm số
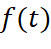 với
với  . Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
. Khảo sát sự biến thiên và vẽ đồ thị của hàm số này. - Hãy giải thích tại sao nồng độ chất khử trùng tăng theo
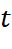 nhưng không vượt ngưỡng 0,5 gam/lít.
nhưng không vượt ngưỡng 0,5 gam/lít.
Giải nhanh:
a. Thể tích nước trong bể sau ![]() phút là:
phút là: ![]() (lít)
(lít)
Khối lượng chất khử trùng có trong bể sau ![]() phút là:
phút là: ![]() (gam)
(gam)
Nồng độ chất khử trùng trong bể sau ![]() phút là:
phút là:  (gam/lít)
(gam/lít)
b. ![]() .
.

![]()
Tiệm cận:  .
.
=>  là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.


Đồ thị:
Hàm số đi qua ba điểm ![]() ;
;  ;
;  .
.

c. Vì  ,
, ![]() và
và 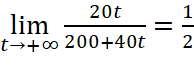 nên nồng độ chất khử trùng tăng theo
nên nồng độ chất khử trùng tăng theo ![]() nhưng không vượt ngưỡng 0,5 gam/lít.
nhưng không vượt ngưỡng 0,5 gam/lít.
Luyện tập 3: Khảo sát sự biến thiên và vẽ đồ thị của hàm số  ..
..
Giải nhanh:
 .
.
Sự biến thiên:
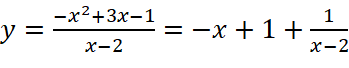

![]() .
.
Hàm số không có cực trị.
Tiệm cận:
 ;
;
Vậy hàm số không có tiệm cận ngang.
 ;
;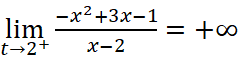
Vậy hàm số có một tiệm cận đứng là đường thẳng ![]() .
.
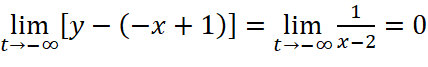 ;
;
Vậy hàm số có một tiệm cận xiên là đường thẳng ![]() .
.

Đồ thị:
- Giao điểm của đồ thị hàm số với trục tung là
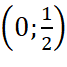
- Giao điểm của đồ thị hàm số với trục hoành là
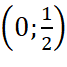 và
và
- Đồ thị hàm số nhận giao điểm có tọa độ
 của đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
của đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.

GIẢI BÀI TẬP
Bài 1.21 trang 32 sách toán 12 tập 1 kntt
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
 ;
;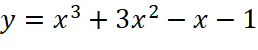 .
.
Giải nhanh:
a. ![]() .
.
Sự biến thiên:
 ;
; ![]() (thỏa mãn)
(thỏa mãn)

Giới hạn tại vô cực:
 ;
;
Đồ thị:

Giao điểm của đồ thị hàm số với trục tung là ![]() .
.
Các điểm ![]() ,
, ![]() thuộc đồ thị hàm số.
thuộc đồ thị hàm số.
Đồ thị hàm số có tâm đối xứng là điểm ![]() .
.
b.
![]() .
.
Sự biến thiên:
Ta có:  ;
;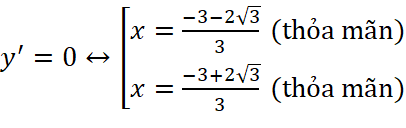
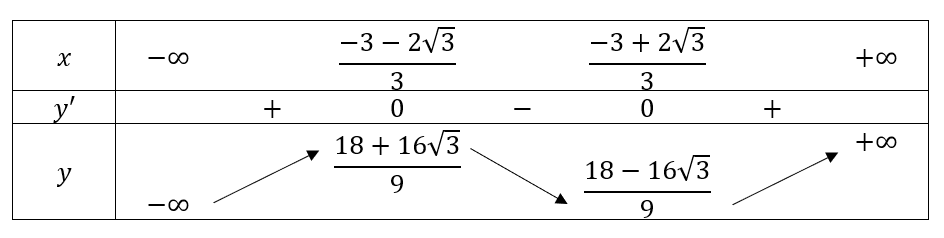
Giới hạn tại vô cực:
 ;
;

Đồ thị:
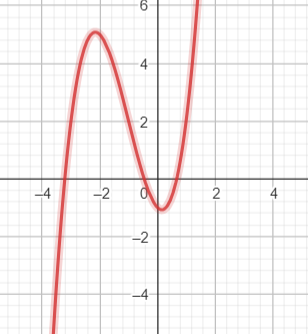
Giao điểm của đồ thị hàm số  với trục tung là
với trục tung là ![]() .
.
Các điểm ![]() ;
; ![]() thuộc đồ thị hàm số
thuộc đồ thị hàm số  .
.
Đồ thị hàm số có tâm đối xứng là điểm ![]() .
.
Bài 1.22 trang 32 sách toán 12 tập 1 kntt
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
 ;
;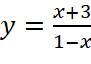 .
.
Giải nhanh:
a.
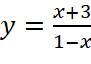 .
.
Sự biến thiên: 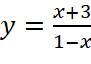
![]() .
.
 ;
;  .
.
 ;
;  .
.
=> Đồ thị hàm số nhận đường thẳng ![]() làm tiệm cận đứng và đường thẳng
làm tiệm cận đứng và đường thẳng
![]() làm tiệm cận ngang.
làm tiệm cận ngang.

Đồ thị: Giao điểm của đồ thị hàm số với trục tung là ![]() .
.
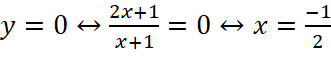
Giao điểm của đồ thị hàm số với trục hoành là 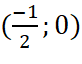 .
.
Đồ thị hàm số nhận giao điểm ![]() của đường tiệm cận làm tâm đối xứng và nhận hai đường phân của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
của đường tiệm cận làm tâm đối xứng và nhận hai đường phân của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.

b.
![]() .
.
Sự biến thiên:
 với
với ![]()
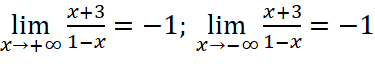
 ;
; 
Do đó đồ thị hàm số nhận đường thẳng ![]() làm tiệm cận đứng và đường thẳng
làm tiệm cận đứng và đường thẳng ![]() làm tiệm cận ngang.
làm tiệm cận ngang.

Đồ thị:
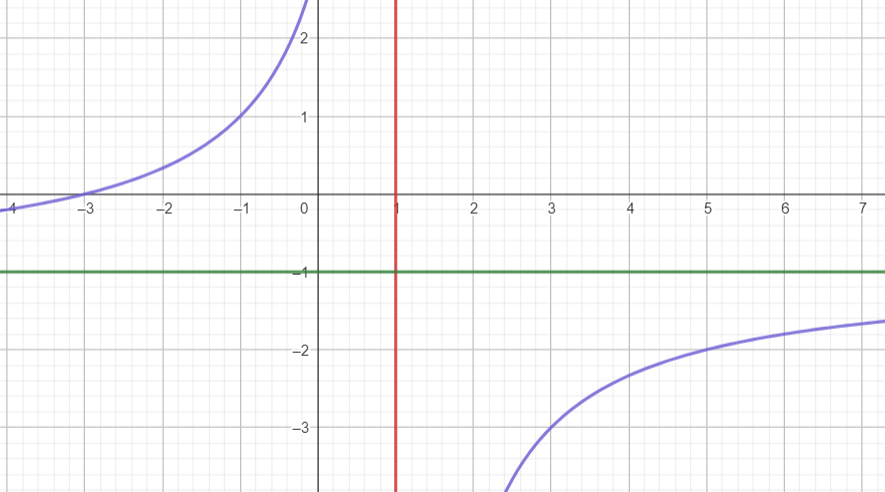
Giao điểm của đồ thị hàm số với trục tung là 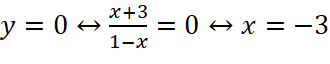 .
.
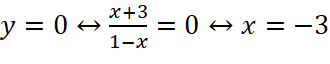
Giao điểm của đồ thị hàm số với trục hoành là ![]()
Đồ thị hàm số nhận giao điểm ![]() của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
Bài 1.23 trang 32 sách toán 12 tập 1 kntt
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
 ;
; .
.
Giải nhanh:
a.
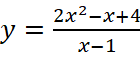 .
.
Sự biến thiên:
Ta có  ;
; 
 ;
; 
Vậy đồ thị không có tiệm cận ngang.
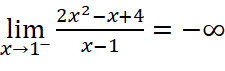 ;
;
Vậy đồ thị có một tiệm cận đứng là đường thẳng ![]() .
.

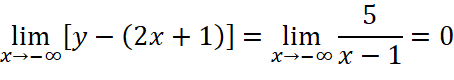
Vậy đồ thị có một tiệm cận xiên là đường thẳng ![]() .
.

Đồ thị:

Giao điểm của đồ thị hàm số với trục tung là điểm ![]() .
.
Đồ thị hàm số không cắt trục hoành.
Đồ thị hàm số nhận giao điểm ![]() của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
b.
![]() .
.
Sự biến thiên:
Ta có:  ;
;
 ;
;
Vậy hàm số không có tiệm cận ngang.
 ;
;
Vậy hàm số có một tiệm cận đứng là ![]() .
.
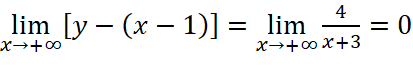 ;
;
Vậy hàm số có một tiệm cận xiên là ![]() .
.

Đồ thị:

Giao điểm của đồ thị với trục tung là  .
.
Giao điểm của đồ thị với trục tung là ![]() .
.
Đồ thị hàm số nhận giao điểm ![]() của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
Bài 1.24 trang 32 sách toán 12 tập 1 kntt
Một cốc chứa ![]() ml dung dịch KOH (potassium hydroxide) với nồng độ 100 mg/ml. Một bình chứa dung dịch KOH khác với nồng độ 8 mg/ml được trộn vào cốc.
ml dung dịch KOH (potassium hydroxide) với nồng độ 100 mg/ml. Một bình chứa dung dịch KOH khác với nồng độ 8 mg/ml được trộn vào cốc.
- Tính nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa, ký hiệu là
 .
. - Coi
 là hàm số xác định với
là hàm số xác định với 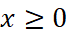 . Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
. Khảo sát sự biến thiên và vẽ đồ thị của hàm số này. - Giải thích tại sao nồng độ KOH trong cốc giảm theo
 nhưng luôn lớn hơn 8 mg/ml.
nhưng luôn lớn hơn 8 mg/ml.
Giải nhanh:
a. Tổng khối lượng KOH sau khi trộn là: ![]() (mg)
(mg)
Tổng thể tích dung dịch sau khi trộn là: ![]() (ml)
(ml)
Nồng độ KOH trong cốc sau khi trộn là:  (mg/ml)
(mg/ml)
b.
![]() .
.
Sự biến thiên:
Ta có:  với
với ![]() .
.
Tiệm cận:
Vậy hàm số có một tiệm cận ngang là đường thẳng ![]()

Đồ thị:

Hàm số giao với trục ![]() tại điểm
tại điểm ![]() .
.
Hàm số đi qua các điểm  và
và ![]() .
.
c. Vì 
![]() và
và  nên nồng độ KOH trong cốc giảm theo
nên nồng độ KOH trong cốc giảm theo ![]() nhưng luôn lớn hơn
nhưng luôn lớn hơn ![]() mg/ml.
mg/ml.
Bài 1.25 trang 32 sách toán 12 tập 1 kntt
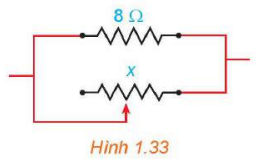
Trong Vật lí, ta biết rằng khi mắc song song hai điện trở ![]() và
và ![]() thì điện trở tương đương
thì điện trở tương đương ![]() của mạch điện được tính theo công thức
của mạch điện được tính theo công thức  (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).
(theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).
Giả sử một điện trở 8 Ω được mắc song song với một biến trở như Hình 1.33. Nếu điện trở đó được kí hiệu là ![]() (Ω) thì điện trở tương đương
(Ω) thì điện trở tương đương ![]() là hàm số của
là hàm số của ![]() . Vẽ đồ thị của hàm số
. Vẽ đồ thị của hàm số ![]() và dựa vào đồ thị đã vẽ, hãy cho biết:
và dựa vào đồ thị đã vẽ, hãy cho biết:
- Điện trở tương đương của mạch thay đổi thế nào khi
 tăng.
tăng. - Tại sao điện trở tương đương của mạch không bao giờ vượt quá 8 Ω.
Giải nhanh:
Ta có:  ,
,![]()
![]() .
.
Sự biến thiên:
 với
với ![]() .
.
Tiệm cận:
 => đồ thị hàm số có một tiệm cận ngang là
=> đồ thị hàm số có một tiệm cận ngang là ![]() .
.
Đồ thị:
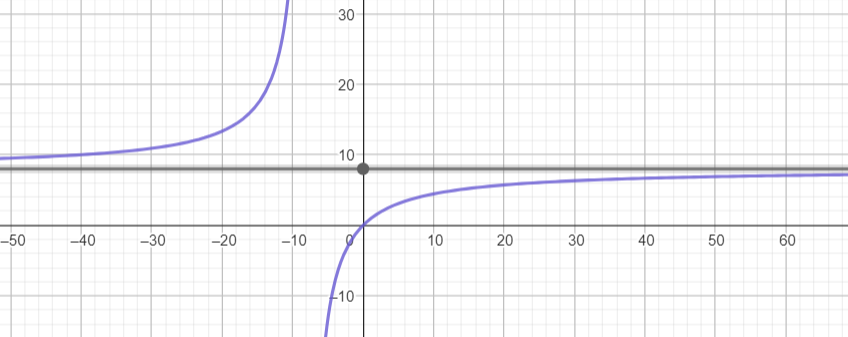
Đồ thị hàm số giao với ![]() và
và ![]() tại gốc tọa độ
tại gốc tọa độ ![]() .
.
Đồ thị hàm số đi qua các điểm  và
và 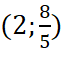 .
.
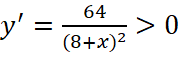
 =>
=>  tăng thì điện trở tương đương của mạch cũng tăng.
tăng thì điện trở tương đương của mạch cũng tăng.
 và
và  => điện trở tương đương của mạch không bao giờ vượt quá
=> điện trở tương đương của mạch không bao giờ vượt quá 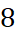 W.
W.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải nhanh Toán 12 kết nối tri thức tập 1, giải nhanh bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số Toán 12 KNTT, Giải Siêu nhanh Toán 12 Kết nối bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận