Giải Siêu nhanh Toán 12 Kết nối bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Giải Siêu nhanh bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số bộ sách Toán 12 kết nối tri thức tập 1. Phần đáp án ngắn gọn, hướng dẫn giải chi tiết cho từng bài tập có trong chương trình học của sách giáo khoa. Hi vọng, các em học sinh hiểu và nắm vững kiến thức môn Toán 12 kết nối tri thức chương trình mới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
1. ĐỊNH NGHĨA
Hoạt động 1: Nhận biết khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
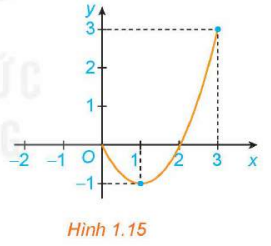
Cho hàm số ![]() với
với ![]() , có đồ thị như Hình 1.15.
, có đồ thị như Hình 1.15.
- Giá trị lớn nhất
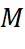 của hàm số trên đoạn
của hàm số trên đoạn 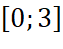 là bao nhiêu? Tìm
là bao nhiêu? Tìm 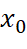 sao cho
sao cho 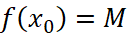 .
. - Giá trị nhỏ nhất
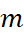 của hàm số trên đoạn
của hàm số trên đoạn  là bao nhiêu? Tìm
là bao nhiêu? Tìm 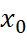 sao cho
sao cho 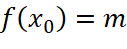 .
.
Giải nhanh:
a. Giá trị lớn nhất của hàm số trên đoạn ![]() là
là ![]() .
.
Tại ![]() thì
thì ![]() .
.
b. Giá trị nhỏ nhất của hàm số trên đoạn ![]() là
là ![]() .
.
Tại ![]() thì
thì ![]() .
.
Luyện tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
 ;
;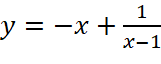 trên khoảng
trên khoảng 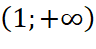 .
.
Giải nhanh:
- Tập xác định của hàm số là
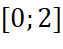 .
.
Với ![]() , ta có:
, ta có: 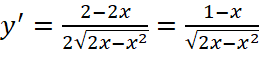 ;
;
![]() (thỏa mãn)
(thỏa mãn)
=> 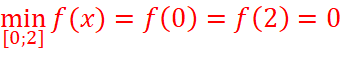 ;
; 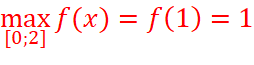
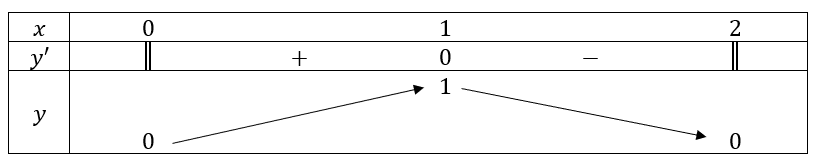
- Với
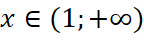 , ta có:
, ta có: 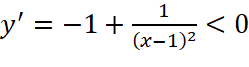 với
với 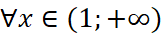 ;
;
 ;
;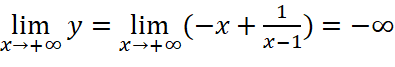
Vậy hàm số không có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn ![]() .
.
2. CÁCH TÌM GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ TRÊN MỘT ĐOẠN
Hoạt động 2: Hình thành các bước tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn.
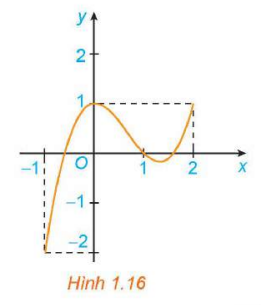
Xét hàm số  trên đoạn
trên đoạn ![]() , với đồ thị như Hình 1.16.
, với đồ thị như Hình 1.16.
- Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn
 .
. - Tính đạo hàm
 và tìm các điểm
và tìm các điểm  mà
mà  .
. - Tính giá trị của hàm số tại hai đầu mút của đoạn
 và tại các điểm
và tại các điểm  đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với
đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với  , số lớn nhất trong các giá trị này với
, số lớn nhất trong các giá trị này với  .
.
Giải nhanh:
. 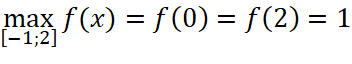 ;
;
.  ;
;
a. ![]() , ta có:
, ta có:  ;
;
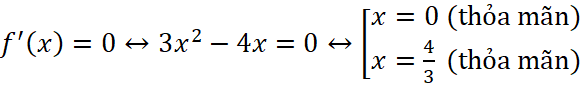
Vậy tại các điểm ![]() hoặc
hoặc 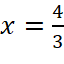 thì
thì ![]() .
.
b. Ta có:
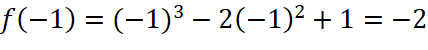 ;
;  ;
;
![]() ;
;  .
.
=> Trong các số trên, số có giá trị nhỏ nhất là ![]() , số có giá trị lớn nhất là
, số có giá trị lớn nhất là ![]() .
.
Vậy 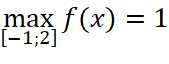 ;
;  .
.
Luyện tập 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
 trên đoạn
trên đoạn 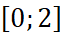 ;
; trên đoạn
trên đoạn  .
.
Giải nhanh:
a.  ;
;
 => Hàm số đồng biến trên đoạn
=> Hàm số đồng biến trên đoạn ![]() .
.
=>  ;
;  .
.
b. ![]() ;
;
![]() :
: ![]() (thỏa mãn)
(thỏa mãn)
 ;
; ![]() ;
;
=> 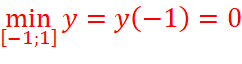 ;
;  .
.
Vận dụng: Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số 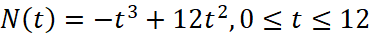 , trong đó
, trong đó ![]() là số người bị nhiễm bệnh (tính bằng trăm người) và
là số người bị nhiễm bệnh (tính bằng trăm người) và ![]() là thời gian (tuần).
là thời gian (tuần).
- Hãy ước tính số người tối đa bị nhiễm bệnh ở địa phương đó.
- Đạo hàm
 biểu thị tốc độ lây lan của virus (còn gọi là tốc độ truyền bệnh). Hỏi virus sẽ lây lan nhanh nhất khi nào?
biểu thị tốc độ lây lan của virus (còn gọi là tốc độ truyền bệnh). Hỏi virus sẽ lây lan nhanh nhất khi nào?
Giải nhanh:
a. ![]() , ta có:
, ta có:
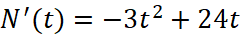 ;
;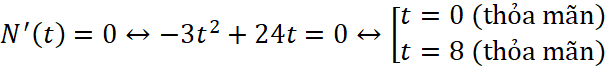
Ta có: ![]() ;
;  ;
;  .
.
Do đó số người tối đa bị nhiễm bệnh ở địa phương đó là 256 người.
b. ![]() , ta có:
, ta có:
 ;
; 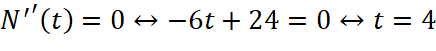 (thỏa mãn)
(thỏa mãn)
![]() ;
; 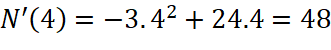 ;
; 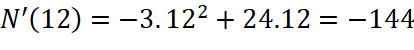 .
.
Do đó virus sẽ lây lan nhanh nhất sau 4 tuần (![]() ).
).
GIẢI BÀI TẬP
Bài 1.10 trang 19 sách toán 12 tập 1 kntt
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
 ;
; trên
trên  ;
; trên
trên 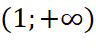 ;
;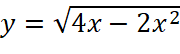 .
.
Giải nhanh:
a. : ![]() .
.
![]() ;
; ![]() (thỏa mãn)
(thỏa mãn)
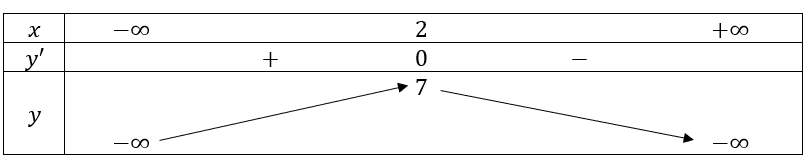
=> ![]() và hàm số không có giá trị nhỏ nhất.
và hàm số không có giá trị nhỏ nhất.
b. Tập xác định: ![]() .
.
Với ![]() , ta có:
, ta có:
 ;
;
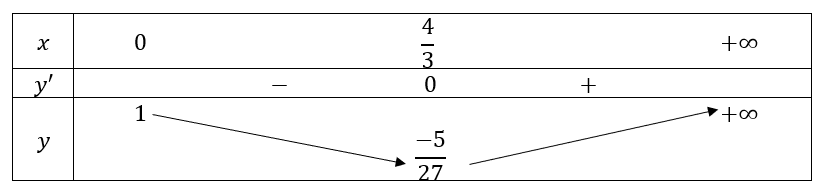
=> 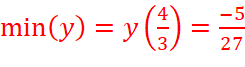 và hàm số không có giá trị lớn nhất.
và hàm số không có giá trị lớn nhất.
c. ![]() , ta có:
, ta có:
 ;
;
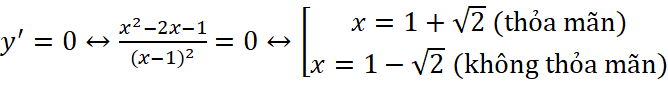

=> 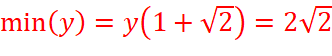 và hàm số không có giá trị lớn nhất.
và hàm số không có giá trị lớn nhất.
d. ![]() .
.
 ;
; 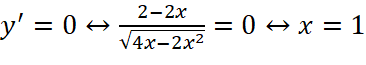 (thỏa mãn)
(thỏa mãn)
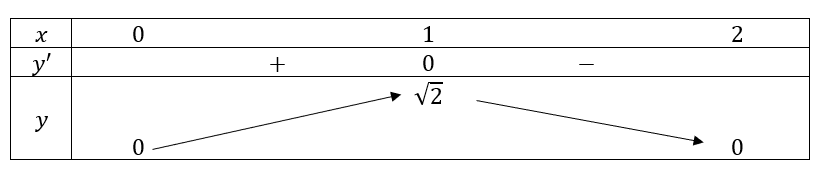
=> ![]() và
và  .
.
Bài 1.11 trang 19 sách toán 12 tập 1 kntt
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
 ;
;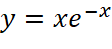 ;
;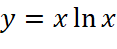 ;
; .
.
Giải nhanh:
a. ![]() .
.
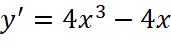 ;
;
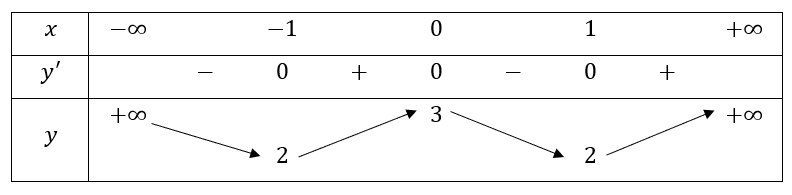
=> ![]() và
và ![]()
b. ![]() .
.
Ta có: ![]() ;
;
![]() (thỏa mãn)
(thỏa mãn)

=> 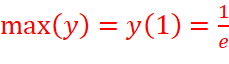 và hàm số không có giá trị nhỏ nhất.
và hàm số không có giá trị nhỏ nhất.
c. ![]() .
.
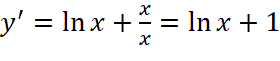 ;
;
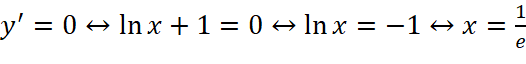 (thỏa mãn)
(thỏa mãn)
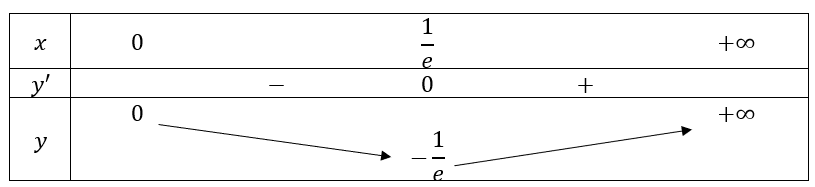
=>  và hàm số không có giá trị lớn nhất.
và hàm số không có giá trị lớn nhất.
d. ![]() .
.
 ;
;
 (thỏa mãn)
(thỏa mãn)
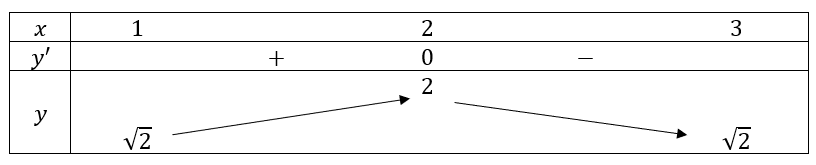
=> 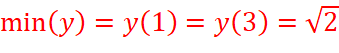 và
và ![]() .
.
Bài 1.12 trang 19 sách toán 12 tập 1 kntt
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
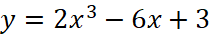 trên đoạn
trên đoạn 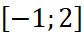 ;
; trên đoạn
trên đoạn 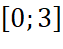 ;
; trên đoạn
trên đoạn  ;
;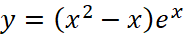 trên đoạn
trên đoạn  .
.
Giải nhanh:
a. ![]() , ta có:
, ta có:
 ;
;  (thỏa mãn)
(thỏa mãn)
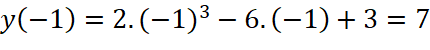 ;
;  ;
;

=>  ;
;  .
.
b. ![]() , ta có:
, ta có:
 ;
;
![]() ;
; 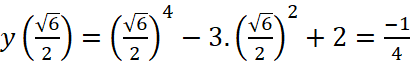 ;
;
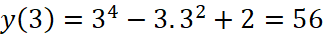
=> 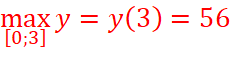 ;
; 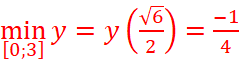 .
.
c. ![]() , ta có:
, ta có:
![]() ;
;

Mà  và
và
![]() ;
;  ;
;
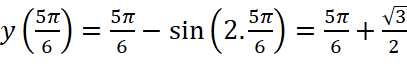 ;
;![]()
=> 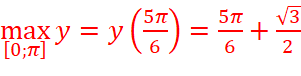 ;
; 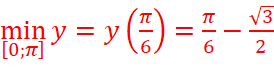 .
.
d. ![]() , ta có:
, ta có:
 ;
;
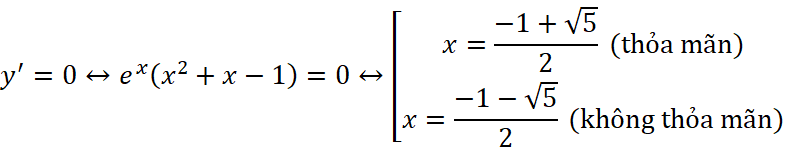
![]() ;
;  ;
;![]()
=> 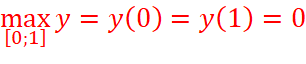 ;
;  .
.
Bài 1.13 trang 19 sách toán 12 tập 1 kntt
Trong các hình chữ nhật có chu vi là 24 cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Giải nhanh:
Gọi chiều dài của hình chữ nhật là ![]() (cm) và
(cm) và ![]()
![]() chiều rộng là
chiều rộng là ![]() (cm).
(cm).
![]()
 (cm2)
(cm2)
![]() ,
, ![]() ;
;
![]() (thỏa mãn)
(thỏa mãn)

=>  .
.
Bài 1.14 trang 19 sách toán 12 tập 1 kntt
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng 108 cm2 như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.

Giải nhanh:
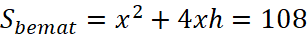 (cm2) →
(cm2) → 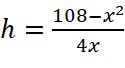 (cm)
(cm)
→ 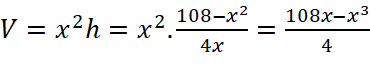 (cm3)
(cm3)
![]() , ta có:
, ta có:
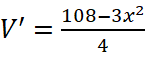 ;
; 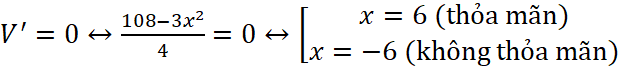

=> (cm3) với
(cm3) với ![]() cm và
cm và  (cm)
(cm)
Bài 1.15 trang 19 sách toán 12 tập 1 kntt
Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích 1000 cm3. Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,2 nghìn đồng/cm2, trong khi mặt bên của bình được làm bằng vật liệu có giá 0,75 nghìn đồng/cm2. Tìm các kích thước của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.
Giải nhanh:
Gọi bán kính của hai đáy bình là ![]() (cm), chiều cao của bình là
(cm), chiều cao của bình là ![]() (cm)
(cm) ![]() ).
).
 (cm3) =>
(cm3) =>  (cm)
(cm)
Gọi chi phí vật liệu sản xuất một chiếc bình là:
 (nghìn đồng)
(nghìn đồng)
![]() , ta có:
, ta có: 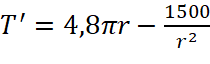 ;
;
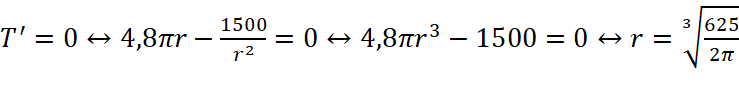 (thỏa mãn)
(thỏa mãn)

=>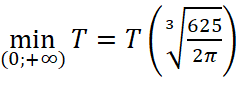
=> chi phí min khi bán kính mặt đáy là 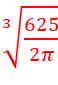 cm và chiều cao là
cm và chiều cao là 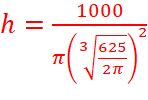 cm.
cm.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải nhanh Toán 12 kết nối tri thức tập 1, giải nhanh bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 KNTT, Giải Siêu nhanh Toán 12 Kết nối bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận