Đề thi toán 7 kết nối tri thức

Đề thi cuối kì 2 toán 7 KNTT: Đề tham khảo số 11

Đề tham khảo số 11 cuối kì 2 Toán 7 Kết nối tri thức gồm nhiều câu hỏi ôn tập hay, các dạng bài tập phong phú giúp các em củng cố ôn luyện lại kiến thức thật tốt chuẩn bị tốt cho kì thi sắp tới. Tài liệu có kèm theo đáp án và lời giải chi tiết. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt điểm cao. Thầy cô và các em kéo xuống để tham khảo ôn luyện

PHÒNG GD & ĐT ……………….

Chữ kí GT1: ...........................

TRƯỜNG THCS……………….

Chữ kí GT2: ...........................

ĐỀ KIỂM TRA CUỐI HỌC KÌ 2

TOÁN 7 – KẾT NỐI TRI THỨC

NĂM HỌC: 2022 - 2023

Thời gian làm bài: 90 phút (Không kể thời gian phát đề)

Họ và tên: ……………………………………  Lớp:  ………………..

Số báo danh: …………………………….……Phòng KT:…………..

Mã phách

 

 

 

 

Điểm bằng số

 

 

 

 

Điểm bằng chữ

Chữ ký của GK1

Chữ ký của GK2

Mã phách

 

A. PHẦN TRẮC NGHIỆM (3 điểm)

Khoanh tròn vào chữ cái đứng trước câu trả lời đúng:

Câu 1. Biểu thức nào sau đây là đơn thức?

A. x.y.HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)C. x + y.D. x – y.

Câu 2. Bậc của đơn thức 2xy7 là

A. 2.B. 7.C. 8.D. 9.

Câu 3. Chọn ngẫu nhiên một số trong tập hợp {2; 3; 5; 6}. Biến cố chắc chắn là:

A. Số được chọn là số nguyên tố

B. Số được chọn nhỏ hơn 7

C. Số được chọn là số chính phương

D. Số được chọn là số chẵn

Câu 4. Trong các biến cố sau em hãy chỉ ra biến cố không thể:

A. Tháng hai năm sau có 31 ngày.

B. Khi gieo con xúc xắc thì số chấm xuất hiện là 6

C. Trong điều kiện bình thường nước đun đến 100 độ sẽ sôi.

D. Ngày mai mặt trời mọc đằng Đông.

Câu 5.  Cho tam giác ABC, AB > AC > BC thì khẳng định nào sau đây đúng?

A. HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)                        B. HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)            C. HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)                        D.HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

Câu 6. Cho HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) có HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023), HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023). Khi đó ta có: 

A.HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)B.HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)C.HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)D.HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

Câu 7. Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây là ba cạnh của một tam giác?

A. 2cm; 3cm; 6cm.B. 3cm; 2cm; 5cm.C. 2cm; 4cm; 6cm.D. 2cm; 3cm; 4cm.

Câu 8.Tam giác ABC có AB = 2cm; BC = 5cm; AC = b (cm) (b là số nguyên). Giá trị của b là:

A.HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) B.HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)C.HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)D.HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

Câu 9. Mặt bên của hình lăng trụ đứng tam giác là

A. Hình tam giácC. Hình chữ nhật
B. Hình thoiD. Hình lục giác đều

Câu 10. Hình lập phương có bao nhiêu đỉnh:

A. HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)B. HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)C.HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)D. HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

Câu 11. Hình hộp chữ nhật có bao nhiêu mặt :

A. HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)B. HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)C. HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)D. HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

Câu 12.Các cạnh bên của hình lăng trụ đứng

A. Song song và không bằng nhauC. Vuông góc với nhau
B. Cắt nhauD. Song song và bằng nhau

B. PHẦN TỰ LUẬN (7 điểm)

Bài 1. (2,0 điểm). Cho biểu thức: HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023).

a) Rút gọn biểu thức HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023), rồi sắp xếp các hạng tử theo luỹ thừa giảm dân của biến HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023).

b) Tính giá trị của biểu thức HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) với HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023).

c) Tính HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) với HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) và HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023).

Bài 2. (1,0 điểm). An và Chi có số bi lần lượt tỉ lệ với 4; 5. Biết rằng An có số bi ít hơn Chi là 4 viên. Tính số viên bi của mỗi bạn.

Bài 3. (1,0 điểm) 

Một hộp có 10 lá thăm có kích thước giống nhau được đánh số thứ tự từ 1 đến 10 . Lấy ngẫu nhiên 1 lá thăm từ hộp. Tính xác suất của các biến cố sau:

A: "Lấy được lá thăm có đánh số 1 ";

B: "Lấy được lá thăm có đánh số chẵn".

Bài 4. (2,5 điểm) Cho HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)cân tại M HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023). Kẻ NH HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MP HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023), PK HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MN HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023). NH và PK cắt nhau tại E.

          a) Chứng minh HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

          b) Chứng minh HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)ENP cân.

          c) Chứng minh ME là đường phân giác của góc NMP.                       

Bài 5. (0,5 điểm) Cho ba số HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) khác HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) thỏa mãn HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023). 

Tính giá trị biểu thức HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

BÀI LÀM

         …………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

……………………………………………………………………………………………………

………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

 

BÀI LÀM:

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

…………………………………………………………………………………………………

TRƯỜNG THCS ........

HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

MÔN: TOÁN 7 – KẾT NỐI TRI THỨC 

A. PHẦN TRẮC NGHIỆM: (3,0 điểm) 

Mỗi câu trả lời đúng được 0,25 điểm. 

1. A

2. C3. B4. A5. A6. C

7. D

8. A9. A10. D11. B12. D

B. PHẦN TỰ LUẬN: (7,0 điểm)

Câu

Ý

Nội dung đáp án

Điểm

1

(2đ)

a

HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) 

HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) 

 

0,75

b

           HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

            HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

                HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

0,75

c

              HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

           HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

 

0,5

2

(1đ)

Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)). Theo đề bài ta có HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)= 4 => x = 16 ; y= 20

Vậy An có 16 viên bi, Chi có 20 viên bi

 

 

1,0

3

(1 điểm)

a)  HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

0,5

b)  HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

 

0,5

4

(2,5 điểm)

a

HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

 a) Xét HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)NHP và HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)PKN vuông tại H và K

             Có NP là cạnh chung

            Có HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) (Vì HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MNP cân tại M(gt))

   => HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)NHP  = HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)PKN (ch-gn)

   =>   NH = PK  (đpcm)

 

b

b) Vì HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)NHP  = HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)PKN (cmt)

  =>  HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

  =>  HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)ENP cân tại E (đpcm)

 

c

c) Ta có MK = MN – KN  (vì K thuộc MN)

              MH = MP – HP     (Vì H thuộc MP)

    Mà MN = MP (Vì HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MNP cân tại M (gt))

           KN = HP (Là hai cạnh tương ứng của HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)NHP  = HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)PKN (cmt))

    =>    MK = MH

    Xét HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MEK và HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MEH  vuông tại K và H (gt)

      Có ME là cạnh chung

      Có MK = MH (cmt)

      =>   HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MEK = HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MEH (ch-cgv)

      =>  HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

      =>  ME là phân giác của góc NMP (đpcm)

4

(0,5 điểm)

 

Ta có HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

Nếu HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) thì HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) thì 

HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023).

0,25

Nếu HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023), áp dụng tính chất dãy tỉ số bằng nhau ta được

HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

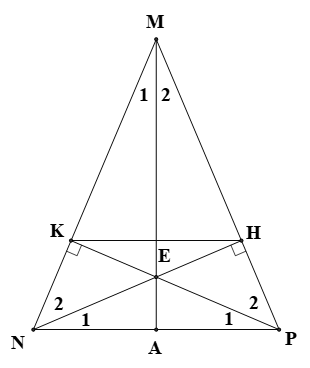HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) nên HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023). 

Do đó HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023).

Vậy hoặc HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023) hoặc HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)MÔN: TOÁN 7 – KẾT NỐI TRI THỨC A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu trả lời đúng được 0,25 điểm. 1. A2. C3. B4. A5. A6. C7. D8. A9. A10. D11. B12. DB. PHẦN TỰ LUẬN: (7,0 điểm)CâuÝNội dung đáp ánĐiểm1(2đ)a   0,75b                                       0,75c                          0,52(1đ)Gọi số bi của An và Chi lần lượt là x và y ( viên bi x, y ). Theo đề bài ta có và y - x = 4. Áp dụng tính chất cảu dãy tỉ số bằng nhau ta có = 4 => x = 16 ; y= 20Vậy An có 16 viên bi, Chi có 20 viên bi  1,03(1 điểm)a)  0,5b)   0,54(2,5 điểm)a a) Xét NHP và PKN vuông tại H và K             Có NP là cạnh chung            Có (Vì MNP cân tại M(gt))   => NHP  = PKN (ch-gn)   =>   NH = PK  (đpcm) bb) Vì NHP  = PKN (cmt)  =>    =>  ENP cân tại E (đpcm) cc) Ta có MK = MN – KN  (vì K thuộc MN)              MH = MP – HP     (Vì H thuộc MP)    Mà MN = MP (Vì MNP cân tại M (gt))           KN = HP (Là hai cạnh tương ứng của NHP  = PKN (cmt))    =>    MK = MH    Xét MEK và MEH  vuông tại K và H (gt)      Có ME là cạnh chung      Có MK = MH (cmt)      =>   MEK = MEH (ch-cgv)      =>        =>  ME là phân giác của góc NMP (đpcm)4(0,5 điểm) Ta có Nếu thì thì .0,25Nếu , áp dụng tính chất dãy tỉ số bằng nhau ta được nên . Do đó .Vậy hoặc hoặc .0,25TRƯỜNG THCS .........MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023).

0,25

TRƯỜNG THCS .........

MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 (2022 – 2023)

MÔN: TOÁN 7 KNTT

 

CHỦ ĐỀ

MỨC ĐỘ

Tổng số câu

 

Điểm số

Nhận biết

Thông hiểu

Vận dụng

VD cao

TN

TL

TN

TL

TN

TL

TN

TL

TN

TL

CVI. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ

 

 

 

 

 

1

(C2 – 1 điểm)

 

 

0

1

TN: 0

TL: 1

CVII. BIỂU THỨC ĐẠI SỐ VÀ ĐA THỨC MỘT BIẾN

 

2

 

 

2

(C1a,b – 1,5đ 

 

1

(C1c-0,5 đ)

 

1

(C4 -  0,5 điểm)

2

4

TN: 0,5

TL: 2,5

CHƯƠNG VIII

LÀM QUEN VỚI BIẾN CỐ VÀ XÁC SUẤT CỦA BIẾN CỐ 

 

 

2

 

 

1

(C3 – 1 điểm)

 

 

2

1

TN: 0,5

TL: 1

CHƯƠNG IX.

 

QUAN HỆ GIỮA CÁC YẾU TỐ TRONG MỘT TAM GIÁC.

 

2

 

2

2

(C4 vẽ hình, ghi gtkl + a – 0,5 + 0,75 đ)

 

1

(C4b,c – 1,25đ)

 

 

4

3

TN: 1

TL: 2,5

CHƯƠNG X. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN

 

4

 

 

 

 

 

 

 

4

0

TN: 1,0

TL: 0

Tổng số câu TN/TL

8

0

4

3

 

3

 

1

12

7

TN: 3

TL: 7

Điểm số

2

 

1

2,75

 

3,75

 

0,5

3

9

 

Tổng số điểm

2 điểm

20 %

3,75 điểm

37,5 %

3,75 điểm

37,5 %

0,5 điểm

5%

10 điểm

100 %

10 điểm

Thêm kiến thức môn học

Giải toán 7 tập 1 kết nối tri thức
Giải toán 7 tập 2 kết nối tri thức
Giải toán 7 kết nối tri thức
Giải SBT toán 7 tập 1 kết nối tri thức
Giải SBT toán 7 tập 2 kết nối tri thức
Giải SBT toán 7 kết nối tri thức
Trắc nghiệm toán 7 kết nối tri thức
Đề thi toán 7 kết nối tri thức
Giáo án Toán 7 kết nối tri thức
Giáo án buổi 2 Toán 7 KNTT
Giáo án điện tử toán 7 kết nối tri thức
Siêu nhanh giải toán 7 kết nối tri thức
5 phút giải toán 7 kết nối tri thức
Slide bài giảng toán 7 kết nối tri thức
Đáp án toán 7 kết nối tri thức
Dễ hiểu giải toán 7 kết nối tri thức
Video bài giảng toán 7 kết nối tri thức
Từ khóa tìm kiếm:

Đề thi cuối kì 2 Toán 7 Kết nối Đề tham khảo số 11, đề thi cuối kì 2 Toán 7 KNTT, đề thi Toán 7 cuối kì 2 Kết nối tri thức Đề tham khảo số 11

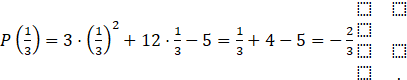
Bình luận

Giải bài tập những môn khác

Giải sgk lớp 7 KNTT

Giải sgk lớp 7 CTST

5 phút giải toán 7 CTST
5 phút soạn bài văn 7 CTST
Văn mẫu 7 CTST

5 phút giải KHTN 7 CTST
5 phút giải lịch sử 7 CTST
5 phút giải địa lí 7 CTST

5 phút giải công nghệ 7 CTST
5 phút giải GDCD 7 CTST
5 phút giải tin học 7 CTST
5 phút giải HĐTN 7 CTST

Giải sgk lớp 7 cánh diều

5 phút giải toán 7 cánh diều
5 phút soạn bài văn 7 cánh diều
Văn mẫu 7 cánh diều

5 phút giải KHTN 7 cánh diều
5 phút giải lịch sử 7 cánh diều
5 phút giải địa lí 7 cánh diều

5 phút giải CN 7 cánh diều
5 phút giải GDCD 7 cánh diều
5 phút giải tin học 7 cánh diều
5 phút giải HĐTN 7 cánh diều

Giải SBT lớp 7 kết nối tri thức

Giải SBT lớp 7 chân trời sáng tạo

Giải SBT lớp 7 cánh diều

Trắc nghiệm 7 Kết nối tri thức

Trắc nghiệm 7 Chân trời sáng tạo

Trắc nghiệm 7 Cánh diêu

Giáo án lớp 7