Soạn giáo án điện tử toán 10 cánh diều bài tập cuối chương III

Nội dung giáo án

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC

KHỞI ĐỘNG

Các en hãy trả lời các câu hỏi trắc nghiệm sau:

Câu 1. Tập xác định của hàm số  là

1. . B.
2. . D. .

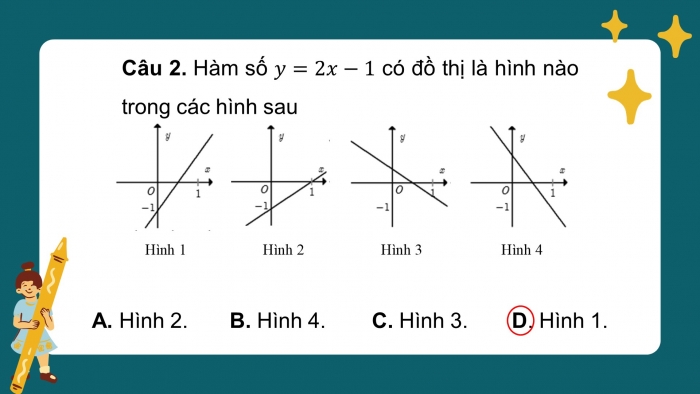
Câu 2. Hàm số  có đồ thị là hình nào trong các hình sau

Câu 3. Hàm số đồng biến trên khoảng nào sau đây?

1. .          B. .
2. .          D. .

Câu 4. Cho parabol . Điểm nào sau đây là đỉnh của ?

1. .                   B. .
2. .           D. .

Câu 5. Bất phương trình  nghiệm đúng với mọi  khi

1. B.           
2. D.

Câu 6. Tập nghiệm của phương trình

1. B.
2. D. .

BÀI TẬP CUỐI CHƯƠNG III

NỘI DUNG BÀI HỌC

Ôn tập kiến thức Chương III

Luyện tập củng cố

1. ÔN TẬP KIẾN THỨC CHƯƠNG III

Đại diện các nhóm lên trình bày sơ đồ tư duy của nhóm

Câu hỏi ôn tập

Cho hàm số bậc hai  có đồ thị , hãy nêu tọa độ đỉnh, trục đối xứng của đồ thị hàm số đó.

Đồ thị là một đường parabol có đỉnh là điểm với toạ độ  và trục đối xứng là đường thẳng .

Với  nêu khoảng đồng biến, nghịch biến của hàm số. Hàm số đạt giá trị nhỏ nhất hay lớn nhất là bao nhiêu, tại  bằng bao nhiêu.

Nếu thì hàm số nghịch biến trên , đồng biến trên

Phát biểu định lí về dấu của tam thức bậc hai.

Trả lời

Cho tam thức bậc hai  , .

+ Nếu  thì  cùng dấu với hệ số  với mọi .

+ Nếu  thì  cùng dấu với hệ số a với mọi

+ Nếu  thì  có hai nghiệm . Khi đó:

cùng dấu với hệ số  với mọi  thuộc các khoảng  và ;  trái dấu với hệ số  với mọi  thuộc khoảng .

Nêu cách giải phương trình dạng  .

Trả lời

(  và  với ,  hoặc  có thể bằng ).

Để giải phương trình , ta làm như sau:

Bước 1. Bình phương hai vế của  dẫn đến phương trình  rồi tìm nghiệm của phương trình này.

Bước 2. Thay từng nghiệm của phương trình  vào bất phương trình  (hoặc ). Nghiệm nào thoả mãn bất phương trình đó thì giữ lại, nghiệm nào không thoả mãn thì loại đi.

Bước 3. Trên cơ sở những nghiệm giữ lại ở Bước 2, ta kết luận nghiệm của phương trình .

1. LUYỆN TẬP – VẬN DỤNG

Bài 1 (SGK – tr.60) Tìm tập xác định của mỗi hàm số sau:

1. a) ; b) ; c) .

Giải

1. a) Biểu thức có nghĩa khi

Vậy tập xác định của hàm số đã cho là