Soạn giáo án điện tử toán 10 cánh diều bài 1: Giá trị lượng giác của một góc từ 0° đến 180°. định lí cosin và định lí sin trong tam giác (4 tiết)

Nội dung giáo án

CHÀO MỪNG CÁC EM ĐẾN VỚI LỚP HỌC!
Cột cờ Lũng Cú là cột cờ Quốc gia, nằm ở đỉnh Lũng Cú hay còn gọi là đỉnh núi Rồng (Long Sơn) thuộc xã Lũng Cú, huyện Đồng Văn, tỉnh Hà Giang, cách cực Bắc Việt Nam khoảng 3,3 km. Thời nhà Lý, cột cờ Lũng Cú chỉ được làm bằng cây sa mộc. Ngày nay, cột cờ có độ cao 33,15 m bao gồm bệ cột cao 20,25 m và cán cờ cao 12,9 m. Chân bệ cột cờ có 8 mặt phù điêu bằng đá xanh mô phỏng hoa văn mặt của trống đồng Đông Sơn và những họa tiết minh họa các giai đoạn qua từng thời kì lịch sử của đất nước, cũng như con người, tập quán của các dân tốc ở Hà Giang. Trên đỉnh cột là Quốc kì Việt Nam có diện tích 54 m2, biểu tượng cho 54 dân tộc của đất nước ta.
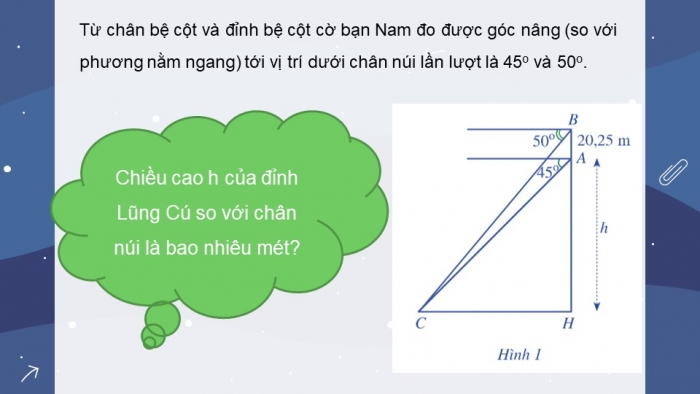
Từ chân bệ cột và đỉnh bệ cột cờ bạn Nam đo được góc nâng (so với phương nằm ngang) tới vị trí dưới chân núi lần lượt là 45o và 50o.
Chiều cao h của đỉnh Lũng Cú so với chân núi là bao nhiêu mét?
CHƯƠNG IV: HỆ THỨC LƯỢNG TRONG TAM GIÁC. VECTƠ
BÀI 1: GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0° ĐẾN 180°. ĐỊNH LÍ COSIN VÀ ĐỊNH LÍ SIN TRONG TAM GIÁC (4 tiết)
I. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0° ĐẾN 180°
HĐ1
Cho tam giác ABC vuông tại A có (ABC) ̂=α
a) Nhắc lại định nghĩa sin⁡α, cos⁡α, tan⁡α, cot⁡α
b) Biểu diễn tỉ số lượng giác của góc 90°-α theo tỉ số lượng giác của góc α
Giải
sin⁡〖α=AC/BC;〗
tan⁡α⁡〖=AC/AB;〗
cot⁡α⁡〖=AB/AC.〗
sin⁡〖(90-α)=cos⁡α;〗
cos⁡(90°-α)⁡〖=sin⁡α;〗
tan⁡(90°-α)⁡〖=cot⁡α;〗
cot⁡(90°-α)⁡〖=tan⁡α;〗
HĐ2
Trong mặt phẳng toạ độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành bán kính R=1 được gọi là nửa đường tròn đơn vị. Với mỗi góc nhọn α ta có thể xác định một điểm M duy nhất trên nửa đường tròn đơn vị sao cho (xOM) ̂=α. Giả sử điểm M có toạ độ (x_0;y_0 ). Hãy tính sin⁡α, cos⁡α, tan⁡α, cot⁡α theo x_0,y_0.
Giải
Xét tam giác vuông OMH, ta có:
sin⁡α=MH/OM=y_0/1=y_0;
cos⁡α=OH/OM=x_0/1=x_0;
tan⁡α=MH/OH=y_0/x_0 ;
cot⁡α=OH/MH=x_0/y_0 ;
Mở rộng khái niệm tỉ số lượng giác đối với góc nhọn cho những góc α từ 0^ođến 180^o, ta có định nghĩa:
Với mỗi góc α (0^o≤α≤180^o ), ta xác định một điểm M(x_o;y_o) trên nửa đường tròn đơn vị sao cho (xOM) ̂=α. Khi đó:
sin⁡ của góc α, kí hiệu là sin⁡α, được xác định bởi: sin⁡α=y_o;
côsin⁡ của góc α, kí hiệu là cos⁡α, được xác định bởi: cos⁡α=x_o;
tang của α, kí hiệu là tan⁡α, được xác định bởi: tanα=y_o/x_o (x_o≠0);
côtang của α, kí hiệu là cot⁡α, được xác định bởi: cot⁡α=x_o/y_o (y_o≠0);
Các số sin⁡α, cos⁡α, tan⁡α, cot⁡α được gọi là giá trị lượng giác của góc α.
Ví dụ 1
Tính các giá trị lượng giác của các góc: 0°, 90°, 180°
Giải
Với α=0°: Khi đó: M trùng với A(1;0).
Do đó sin⁡〖0°=0〗, cos⁡〖0°〗=1; tan⁡〖0°〗=0, cot⁡〖0°〗 không xác định.
Với α=90°: Khi đó: M trùng với B(0;1).
Do đó sin⁡〖90°=1〗, cos⁡〖90°〗=0; tan⁡〖90°〗 không xác định, cot⁡〖90°〗=0.
Với α=180°: Khi đó: M trùng với C(-1;0).
Do đó sin⁡〖180°=0〗, cos⁡〖180°〗=-1; tan⁡〖180°〗=0, cot⁡〖180°〗 không xác định.
Chú ý:
tan⁡α=sin⁡α/cos⁡α (α≠90^o);
cot⁡α=cos⁡α/sin⁡α (0<α<180^o)
⇒tan⁡α=1/cot⁡α (α∉{0^o;90^o;180^o}).
cos⁡( 90^o-α)=sin⁡α (0^o≤α≤90^o );
sin⁡( 90^o-α)=cos⁡α (0^o≤α≤90^o );
tan⁡( 90^o-α)=cot⁡α (0^o<α≤90^o );
cot⁡( 90^o-α)=tan⁡α (0^o≤α<90^o )
HĐ3
Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và (xOM) ̂=α.
a) Chứng minh (xON) ̂=180°-α
b) Biểu diễn giá trị lượng giác của góc 180°-α theo giá trị lượng giác của góc α.
Giải
a) Do MN // Ox nên (NMO) ̂=(xOM) ̂=α (hai góc so le trong).
Xét tam giác OMN cân tại O do OM=ON ta có:
(MON) ̂=180^o-2(NMO) ̂=180-2α
⇒(xON) ̂=(xOM) ̂+(MON) ̂=180^o-α
Kết luận:
Với 0^o≤α≤180^o thì:
sin⁡( 180^o-α)= sin⁡α;
cos⁡( 180^o-α)= cos⁡α;
tan⁡( 180^o-α)=-tan⁡α (α≠90^o);
cot⁡( 180^o-α)=-cot⁡α (α≠90^o,α≠180^o ).
Ví dụ 2
Không dùng máy tính cầm tay, tính giá trị của biểu thức sau:
T=cos⁡〖15°〗-sin⁡〖35°〗+cos⁡〖55°〗+cos⁡〖165°〗-cos⁡〖180°〗
Giải
T=cos⁡〖15°〗-sin⁡〖35°〗+cos⁡〖55°〗+cos⁡〖165°〗-cos⁡〖180°〗
⇔T=cos⁡〖15°〗-sin⁡〖35°〗+cos⁡(90°-35°)+cos⁡(180°-15°)+1
⇔T=cos⁡〖15°〗-sin⁡〖35°〗+sin⁡〖35°〗-cos⁡〖15°〗+1
⇔T=1
Ví dụ 3
Viết giá trị lượng giác của góc 120°
Giải
Ta có:
sin⁡〖120°〗=sin⁡〖60°〗=√3/2
cos⁡〖120°〗=-cos⁡〖60°〗=-1/2
tan⁡〖120°〗=-tan⁡〖60°〗=-√3
cot⁡〖120°〗=-cot⁡〖60°〗=-√3/3
HĐ4
Sử dụng máy tính cầm tay để tính sin⁡〖75°〗, cos⁡〖175°〗, tan⁡〖64°〗
Để tính các giá trị lượng giác trên, sau khi đưa máy tính vầ chế độ “độ” ta làm như sau:
HĐ5
Sử dụng máy tính cầm tay để tìm số đo góc α trong các trường hợp sau
a) cos⁡α=-0,97
b) tan⁡α=0,68
c) sin⁡α=0,45
Chú ý:
Khi tìm góc α(0°≤α≤180°) nếu đã biết sin⁡α, trên máy tính chỉ hiện lên kết quả góc α trong khoảng từ 0° đến 180°.
Luyện tập 1
Hãy tính chiều cao h của đỉnh Lũng Cú so với chân núi trong bài toán ở phần mở đầu.
Giải
Theo tính chất hai đường thẳng song song ta có: {█(&(ACH) ̂=45°@&(BCH) ̂=50°)┤
Ta có {■(tan(ACH) ̂=AH/CH @tan(BCH) ̂=BH/CH)┤ ⇔{■(tan45^°=h/CH @tan50^°=(h+20,25)/CH)┤
Mà CH=AH do tam giác ACH vuông cân tại H.
⇒tan50^°=(h+20,25)/h
⇒h≈105,6 (m)
II. ĐỊNH LÍ CÔSIN
Cho tam giác ABC có BC=a, AC=b, AB=c, (BAC) ̂=α. Kẻ đường cao BH. Thực hiện các hoạt động sau:
HĐ6
Cho α là góc nhọn, chứng minh:
a) HC=|AC-AH| và 〖BC〗^2=〖AB〗^2+〖AC〗^2-2AH.AC
b) a^2=b^2+c^2-2bc cos⁡α
Giải
a) Nếu góc C nhọn thì H nằm giữa A và C.
Do đó
HC=AC-AH=|AC-AH|
Nếu góc C tù thì C nằm giữa A và H. Do đó
HC=AH-AC=|AC-AH|
Nếu góc C vuông thì C trùng với H. Do đó
HC=0=|AC-AH|
Trong mọi trường hợp, ta đều có HC=|AC-AH|
Xét tam giác vuông BHC và AHB, áp dụng định lí Pythagore, ta có:
〖BC〗^2=〖BH〗^2+〖HC〗^2=〖BH〗^2+(AC-AH)^2
=(〖BH〗^2+〖AH〗^2 )+〖AC〗^2-2AH.AC
=〖AB〗^2+〖AC〗^2-2AH.AC
b) Xét tam giác vuông AHB, ta có: AH=AB cos⁡A=c cos⁡α
Do đó 〖BC〗^2=〖AB〗^2+〖AC〗^2-2AH.AC=b^2+c^2-2bc cos⁡α
Vậy a^2=b^2+c^2-2bc cos⁡α
HĐ7
Cho α là góc tù, chứng minh:
a) HC=AC+AH và 〖BC〗^2=〖AB〗^2+〖AC〗^2+2AH.AC
b) a^2=b^2+c^2-2bc cos⁡α
Giải
a) Xét tam giác vuông BHC và AHB, áp dụng định lí Pythagore, ta có:
〖BC〗^2=〖BH〗^2+〖HC〗^2=〖BH〗^2+(AC+AH)^2
=(〖BH〗^2+〖AH〗^2 )+〖AC〗^2+2AH.AC
=〖AB〗^2+〖AC〗^2+2AH.AC
b) Xét tam giác vuông AHB, ta có:
AH=AB cos⁡(180°-α)=-c cos⁡α
Do đó 〖BC〗^2=〖AB〗^2+〖AC〗^2+2AH.AC=b^2+c^2-2bc cos⁡α
Vậy a^2=b^2+c^2-2bc cos⁡α
HĐ8
Cho α là góc vuông. Chứng minh a^2=b^2+c^2-2bc cos⁡α
Áp dụng định lí Pythagore cho tam giác ABC vuông tại A có:
a^2=b^2+c^2
Ta có: cos⁡α=cos 90^o=0⇒2bc cos⁡α=0
⇒a^2=b^2+c^2-2bc cos⁡α
Kết luận:
Cho tam giác ABC có BC=a, CA=b, AB=c. Khi đó:
a^2=b^2+c^2-2bc.cos⁡A
b^2=c^2+a^2-2ca.cos⁡B
c^2=a^2+b^2-2ab.cos⁡C
Lưu ý:
cos⁡A=(b^2+c^2-a^2)/2bc cos⁡B=(a^2+c^2-b^2)/2ac cos⁡C=(a^2+b^2-c^2)/2ab
Ví dụ 4
Cho tam giác ABC có AB=3, AC=5 và A ̂=120°
a) Tính cos⁡A
b) Tính độ dài cạnh BC
Giải
a) Ta có:
cos⁡A=cos⁡〖120°〗=-cos⁡〖60°〗=-1/2
b) Áp dụng định lí côsin trong tam giác ABC, ta có:
〖BC〗^2=〖AB〗^2+〖AC〗^2-2AB.AC.cos⁡A
〖⇔BC〗^2=3^2+5^2-2.3.3.(-1/2)=49
⇒BC=√49=7
Luyện tập 2
Cho tam giác ABC có AB=5, AC=6, BC=7. Tính cos⁡〖A.〗
Giải
cosA=(AC^2+AB^2-BC^2)/(2.AC.AB)=(6^2+5^2-7^2)/2.6.5=1/5
Hai máy bay cùng xuất phát từ một sân bay A và bay theo hai hướng khác nhau, tạo với nhau góc 60°. Máy bay thứ nhất bay với vận tốc 650 km/h, máy bay thứ hai bay với vận tốc 900 km/h. Sau 2 giờ bay, hai máy bay cách nhau bao nhiêu ki-lô-mét (làm tròn kết quả đến hàng phần trăm)? Biết rằng cả 2 máy bay bay theo đường thẳng và sau 2 giờ bay đều chưa hạ cánh.