Bài giảng điện tử chuyên đề Tin học 11 - Khoa học máy tính cánh diều

CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI HỌC NGÀY HÔM NAY! 

KHỞI ĐỘNG 

Trong toán học, n giai thừa (kí hiệu n!) là tích của n số nguyên dương đầu tiên n! = n × (n – 1) × … × 1. Vậy ta có thể dùng công thức sau đây để tính n! được không? 

n!= {█(&n ×(n−1)!nếu n ≥1@&1 nếu n=0                       )┤ 

Công thức có thể dùng tính n! vì:  

Nếu n = 0 → 0! = 1. 

Nếu n   1, n  (n – 1)! = n  (n – 1)  … 1 = n! 

CHUYÊN ĐỀ 1. THỰC HÀNH  

THIẾT KẾ THUẬT TOÁN THEO KĨ THUẬT ĐỆ QUY 

BÀI 1.  

KHÁI NIỆM ĐỆ QUY VÀ VÍ DỤ 

NỘI DUNG BÀI HỌC 

Một số ví dụ về đệ quy 

Khái niệm và các thành phần cơ bản trong định nghĩa đệ quy 

01 MỘT SỐ VÍ DỤ VỀ ĐỆ QUY 

Thảo luận nhóm: Đọc thông tin và thực hiện nhiệm vụ ở mỗi trạm theo nội dung như sau: 

Trạm 1 

Xác định các công thức toán học mang tính đệ quy thông qua đọc thông tin mục 1 trang 5,6 và trả lời câu hỏi 1 phần Hoạt động trang 6 sách CĐHT. 

Trạm 2 

Ví dụ sự vật, sự việc, hiện tượng mang tính đệ quy trong đời sống hàng ngày và mô tả chúng. 

Trong toán học có rất nhiều công thức được định nghĩa thông qua chính nó ở phiên bản nhỏ hơn 

> Công thức mang tính đệ quy 

Ví dụ:  Công thức sinh dãy số Fibonacci 0, 1, 1, 2, 3, 5, 8, 13,… 

F(n) =   

F(n −1)+F(n−2) nếu n≥2 

0 nếu n = 0 

1 nếu n = 1 

(1) 

Hai công thức sau đều được sử dụng để tính số cách chọn k phần từ từ n phần tử:  

C(n, k)=n!/k!(n−k)! 

(2) 

C(n,k)= 

C(n−1,k−1)+C(n−1,k) nếu 0<k<n 

1 nếu k = 0 

1 nếu k = n 

(3) 

Theo em, trong hai công thức (2) và (3), công thức nào là công thức mang tính đệ quy? Em hãy giải thích cho lựa chọn của mình. 

Hướng dẫn thực hiện 

C(n,k)= 

C(n−1,k−1)+C(n−1,k) nếu 0<k<n 

1 nếu k = 0 

1 nếu k = n 

(3) 

→ Sử dụng công thức (3) để tiếp tục tính toán ta có:   

C_n^k=C_n−1  ^k+ C_n−1^k−1 

C_n−1^k=C_n−2  ^k+ C_n−2 ^k−1  … 

Không có điểm dừng 

C_n^0=C_n  ^n= 1 

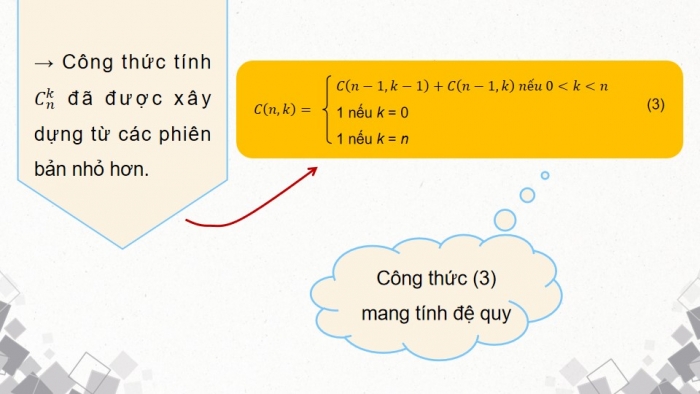
→ Công thức tính C_n^k đã được xây dựng từ các phiên bản nhỏ hơn. 

Công thức (3) mang tính đệ quy 

Trong cuộc sống hằng ngày, có rất nhiều sự việc, hiện tượng, cách giải quyết một vấn đề được mô tả dưới góc nhìn mang tính đệ quy. 

Ví dụ: bộ búp bê Nga Matryoshka 

Hình 1. Bộ búp bê Matryoshka 

Hình 2. Cách đếm số búp của bộ Matryoshka 

02 KHÁI NIỆM VÀ CÁC THÀNH PHẦN CƠ BẢN TRONG ĐỊNH NGHĨA ĐỆ QUY 

2. Hàm dem_Bupbe (búp bê A) ở Hình 3 được sử dụng để mô tả cách đếm số búp bê của bộ Matryoshka một cách đệ quy nếu búp bê A là búp bê lớn nhất của bộ. Em hãy cho biết dấu        trong hàm dem_Bupbe (búp bê A) cần được thay bằng gì.

Hình 3. Hàm mô tả cách đếm búp bê của bộ Matryoshka nếu búp bê A là búp bê lớn nhất của bộ 

Hướng dẫn thực hiện 

def dem_Bupbe (búp bê A): 

      if (không mở được búp bê A): 

          return 

      else: 

          return dem_Bupbe (con của búp bê A) + 

Phần cơ sở 

Phần đệ quy 

3. Xét tập S được định nghĩ đệ quy như sau:

Phần cơ sở: 3 là phần tử của S. 

Phần đệ quy: Nếu x thuộc S và y thuộc S thì x + y thuộc S (chú ý: x và y có thể cùng giá trị). 

Em hãy liệt kê 10 phần tử của tập S. 

 10 phần tử của tập hợp S là:  

S0 = 0; S1 = 1; 

S = {0;1;1;2;2;3;4;5;8;13} 

4. Công thức toán học, dãy số hay hình ảnh nào sau đây được xây dựng mang tính đệ quy? Tại sao?
5. Định nghĩa: Đệ quy của một đối tượng là sự mô tả cách xây dựng đối tượng từ phiên bản nhỏ hơn của chính đối tượng đó. 

Thành phần 

Phần cơ sở: Phần định nghĩa đối tượng khi nó đã ở kích thước nhỏ nhất  

C0=1, C1=1 

Phần đệ quy: Phần chứa quy tắc để xây dựng đối tượng mới từ một đối tượng 

C_n^k=C_n−1  ^k+ C_n−1^k−1 

Trong những câu sau đây, câu nào đúng khi nói về đệ quy? 

1. Ưu điểm của đệ quy là giúp cho mô tả đối tượng, sự việc trở nên ngắn gọn.
2. khi đưa ra định nghĩa đệ quy của một đối tượng, không nhất thiết phải có phần cơ sở.
3. Trong một công thức đệ quy, phần đệ quy đưa ra quy tắc xây dựng đối tượng mới chỉ từ một đối tượng cùng dạng có kích thước nhỏ hơn.
4. Trong một công thức đệ quy, phần cơ sở là phần chứa quy tắc để xây dựng đối tượng mới từ một đối tượng cùng dạng có kích thước nhỏ hơn.

LUYỆN TẬP 

Câu 1. Định nghĩa đệ quy của một đối tượng gồm:   

1. phần cơ sở và phần quy tắc.
2. phần quy tắc và phần định nghĩa.
3. phần cơ sở và phần đệ quy.
4. phần quy tắc và phần đệ quy.

Câu 2. Cho công thức toán học sau: 

x^n={█(&1                 nếu n=0@&x × x^n−1 nếu n>0)┤ 

Phần cơ sở của x^n là: 

...