Giải luyện tập 4 trang 68 sgk Toán 8 tập 2 CD
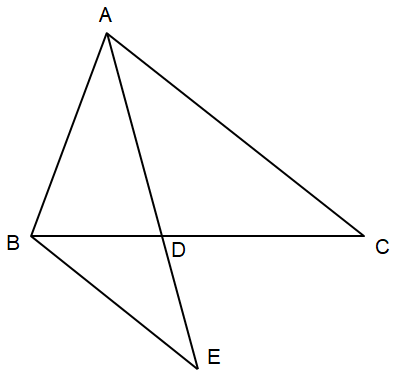
Luyện tập 4: Cho tam giác ABC, điểm D thuộc cạnh BC sao cho $\frac{DB}{DC}=\frac{AB}{AC}$. Chứng minh AD là tia phân giác của góc BAC.
Từ B kẻ đường thẳng song song với AC, cắt AD tại E.
Ta có: $\frac{DB}{DC}=\frac{BE}{AC}$ (BE // AC)
Mà $\frac{DB}{DC}=\frac{AB}{AC}$
Suy ra: $\frac{BE}{AC}=\frac{AB}{AC}$ hay BE = AB.
Do đó tam giác ABE cân tại B nên góc BAD bằng góc BEA.
Mà góc BEA bằng góc DAC (hai góc so le của hai đường thẳng song song)
Suy ra: Góc BAD bằng góc DAC. Do đó, AD là đường phân giác của góc BAC.

Bình luận