Giải bài tập 4 trang 69 sgk Toán 8 tập 2 CD

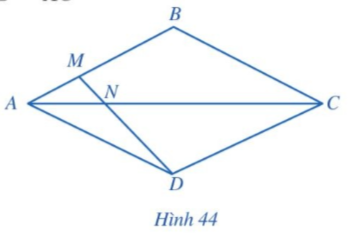
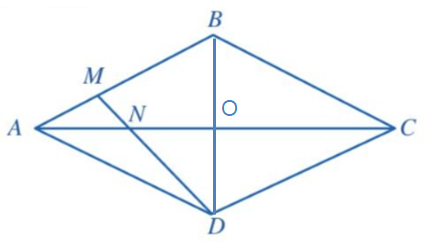
Gọi giao điểm hai đường chéo AC và BD là O.

Vì ABCD là hình thoi nên AC vuông góc với BD tại O.

Tam giác ABD cân tại A có AO là đường cao nên AO cũng là đường phân giác của góc BAD. 

Tam giác AMD có AN là đường phân giác của góc MAD nên $\frac{ND}{MN}=\frac{AD}{AM}$ (1)

Ta có: AM = $\frac{1}{3}$AB mà AD = AB

Suy ra: AM = $\frac{1}{3}$AD. (2)

Từ (1)(2) suy ra: $\frac{ND}{MN}=\frac{AD}{\frac{1}{3}AD}$ hay $\frac{ND}{MN}=3$.

Do đó: ND = 3MN.