Giải câu 3 bài các số đặc trưng đo mức độ phân tán của mẫu số liệu

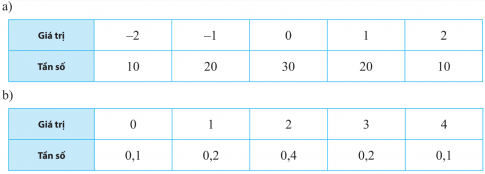
a. Giá trị trung bình của mẫu số liệu trên là: $\frac{1}{90}$[10. (-2) + 20. (-1) + 30. 0 + 20. 1 + 10. 2) = $\frac{1}{9}$

Phương sai của mẫu số liệu trên là:

$S^{2}$ = $\frac{1}{90}$[10.  $(-2)^{2}$ + 20.  $(-1)^{2}$ + 30.  $0^{2}$ + 20.  $1^{2}$ +  10. $2^{2}$ -  $(\frac{1}{9})^{2}$ $\approx$ 1,3

Độ lệch chuẩn của mẫu số liệu trên là: S = $\sqrt{S^{2}}$ $\approx$ $\sqrt{1,3}$ $\approx$ 1,14.

Khoảng biến thiên của mẫu số liệu trên là: R = 2 - (-2) = 4

Cỡ mẫu n = 90, là số chẵn. Khi sắp xếp theo dãy không giảm, số liệu thứ 45, 46 đều là 0, nên giá trị tứ phân vị thứ hai là $Q_{2}$ = 0.

Tứ phân vị thứ nhất là trung vị của mẫu:

Ta thấy cơ mẫu bằng 45, là số lẻ, nên $Q_{1}$ = -1

Tứ phân vị thứ ba là trung vị của mẫu: 

Ta thấy cơ mẫu bằng 45, là số lẻ, nên $Q_{3}$ = 1

Khoảng tứ phân vị của mẫu số liệu trên là: $\Delta_{Q}$ = 1 - (-1) = 2

b. Giá trị trung bình của mẫu số liệu trên là: (0. 0,1 + 1. 0,2 + 2. 0,4 + 3. 0,2 + 4. 0,1): 1 = 2

Phương sai của mẫu số liệu trên là: 

$S^{2}$ = (0,1.  $0^{2}$ + 0,2.  $1^{2}$ + 0,4.  $2^{2}$ + 0,2.  $3^{2}$ +  0,1. $4^{2}$) -  $2^{2}$ = 1,2

Độ lệch chuẩn của mẫu số liệu trên là: S = $\sqrt{S^{2}}$ $\approx$ 1,1

Khoảng biến thiên của mẫu số liệu trên là: 4 - 0 = 4

Ta có: Giá trị tứ phân vị thứ hai là $Q_{2}$ = 2

Giá trị tứ phân vị thứ nhất là $Q_{1}$ = 1; giá trị tứ phân vị thứ ba là $Q_{3}$ = 3

Khoảng tứ phân vị của mẫu số liệu trên là: $\Delta_{Q}$ = 3 - 1 = 2