Giải câu 1 trang 162 toán VNEN 9 tập 2

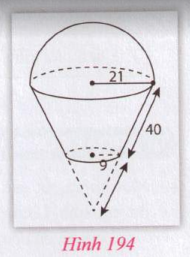
Đường cao của hình nón cụt là: $h = \sqrt{l^2 - (r_1 - r_2)^2} = \sqrt{40^2 - (21-9)^2} = 4\sqrt{91}$ cm

Thể tích và diện tích xung quanh hình nón cụt là:

• $S_{xq1} = \pi \times (r_1 + r_2)\times l = \pi \times (9 + 21)\times 40 = 1200\pi \; cm^2$
• $V_1 = \frac{1}{3} \pi \times h\times (r_1^2+r_2^2+r_1\times r_2) = \frac{1}{3} \pi \times 4\sqrt{91}\times (9^2+21^2+9\times 21) = 948\sqrt{91}\pi \; cm^3$

Thể tích và diện tích xung quanh của nửa hình cầu là:

• $S_{xq2} = \frac{1}{2}\times 4\pi \times r^2 =\frac{1}{2}\times 4\pi \times 21^2  = 882 \pi \; cm^2$
• $V_2 = \frac{1}{2}\times \frac{4}{3} \pi \times r^3 = \frac{1}{2}\times \frac{4}{3} \pi \times 21^3 = 6174\pi \; cm^3$

Diện tích và thể tích của vật là:

• $S = S_{xq1}+ S_{xq2} = 2082\pi \; cm^2$
• $V=V_1+V_2 = (948\sqrt{91}+6174)\pi \; cm^3$