Giải bài tập 64 trang 87 SBT toán 7 tập 2 cánh diều

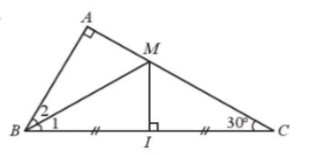
a) Tam giác ABC vuông tại A nên $\widehat{ABC}=90^{\circ}-\widehat{C}$ 

Vì điểm M thuộc đường trung trực của BC nên MB = MC, do đó tam giác MBC cân ở M, ta có $\widehat{B1}=\widehat{C}=30^{\circ}$.

Mặt khác $\widehat{B1}+\widehat{B2}=60^{\circ}$ nên $\widehat{B2}=\widehat{ABC}-\widehat{B1}=30^{\circ}$

Suy ra $\widehat{B2}=\widehat{B1}$

Vậy BM là tia phân giác của góc ABC

b) Gọi I là trung điểm của BC có MI vuông góc với BC

Xét tam giác vuông ABM và IBM có:

BM chung

$\widehat{B2}=\widehat{B1}$

Suy ra $\Delta ABM=\Delta IBM$ (cạnh huyền - góc nhọn)

Suy ra MA = MI

Trong tam giác vuông MIC có MC > MI suy ra MC > MA