Giải bài tập 5 trang 76 SBT toán 10 tập 2 chân trời
Bài tập 5. Một tháp làm nguội của một nhà máy có mặt cắt là hình hypebol có phương trình $\frac{x^{2}}{30^{2}} - \frac{y^{2}}{50^{2}} = 1$. Biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng $\frac{1}{2}$ khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính đáy của tháp.
Trả lời:
Gọi r và R lần lượt là bán kính nóc và bán kính đáy của tháp. Ta tính được khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng 40 m và khoảng cách từ tâm đối xứng đến đáy bằng 80 m
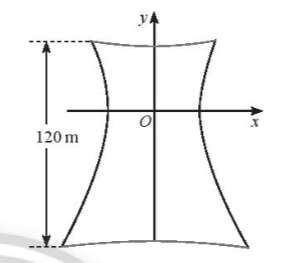
Thay tọa độ 2 điểm M(R; -80) và N(r; 40) vào phương trình hypebol ta tính được:
R = $30\sqrt{1 + \frac{(-80)^{2}}{50^{2}}} \approx 57$ m
r = $30\sqrt{1 + \frac{40^{2}}{50^{2}}} \approx 38$ m
Từ khóa tìm kiếm Google: giải toán 10 chân trời tập 2, giải sách kết nối 10 môn toán tập 2, giải toán sách mới bài 10 tập 2, bài 4 Ba đường conic trong mặt phẳng tọa độ

Bình luận