Giải bài tập 4 trang 94 sgk Toán 8 tập 2 CD
Bài tập 4 trang 94 sgk Toán 8 tập 2 CD: Cho tứ giác ABCD. Tia phân giác của các góc BAD và BCD cắt nhau tại điểm I. Biết I thuộc đoạn thẳng BD (Hình 103). Chứng minh AB . CD = AD . BC.
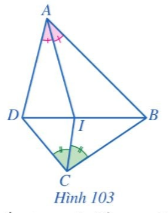
Tam giác ABD có AI là đường phân giác của góc BAD
Suy ra: $\frac{ID}{IB}=\frac{AD}{AB}$ (Tính chất đường phân giác) (1)
Tam giác BCD có CI là đường phân giác của góc BCD
Suy ra: $\frac{ID}{IB}=\frac{CD}{BC}$ (Tính chất đường phân giác) (2)
Từ (1)(2) suy ra: $\frac{AD}{AB}=\frac{CD}{BC}$ hay AB . CD = AD . BC.
Xem toàn bộ: Giải toán 8 Cánh diều bài tập cuối chương VIII
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận