Giải Bài tập 3 trang 72 sgk Toán 8 tập 1 Chân trời
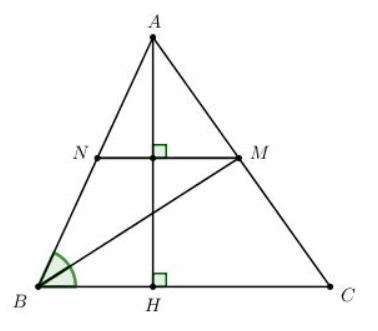
Bài tập 3 trang 72 sgk Toán 8 tập 1 CTST: Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH cắt AB tại N.
a) Chứng minh rằng tứ giác BCMN là hình thang.
b) Chứng mình rằng BN = MN.
a) Ta có: MN⊥AH(gt)
Và BC⊥AH (AH là đường cao của tam giác ABC) ⇒MN//BC
Suy ra BCMN là hình thang
b)$\widehat{NBM}=\widehat{MBC}$ (BM là tia phân giác góc B)
Suy ra $\widehat{BMN}=\widehat{NBM}$⇒ ΔBMN cân tại N.
Vậy BN=MN

Bình luận