Giải bài 9 bài ôn tập cuối năm
Bài tập 9. Cho hàm số y = f(x) = ax2 + bx + c với đồ thị là parabol (P) có đỉnh $I\left ( \frac{5}{2};\frac{1}{4} \right )$ và đi qua điểm A(1; 2).
a. Biết rằng phương trình của parabol có thể viết dưới dạng y = a(x - h)2 + k, trong đó I(h, k) là tọa độ đỉnh của parabol. Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.
b. Từ parabol (P) đã vẽ ở câu a, hãy cho biết khoảng đồng biến và khoảng nghịch biến của hàm số $y = f(x)$.
c. Giải bất phương trình $f(x)$ $\geq $ 0.
a. y = a(x - h)2 + k, mà parabol đi qua điểm $I\left ( \frac{5}{2};\frac{1}{4} \right )$ nên ta có: $y = a\left ( x-\frac{5}{2} \right )^{2}+\frac{-1}{4}$
Mà parabol đi qua A(1; 2) nên: $2 = a\left ( 1-\frac{5}{2} \right )^{2}+\frac{-1}{4}$
$\Rightarrow$ a = 1.
Vậy parabol dạng: y = x2 -5x +6.
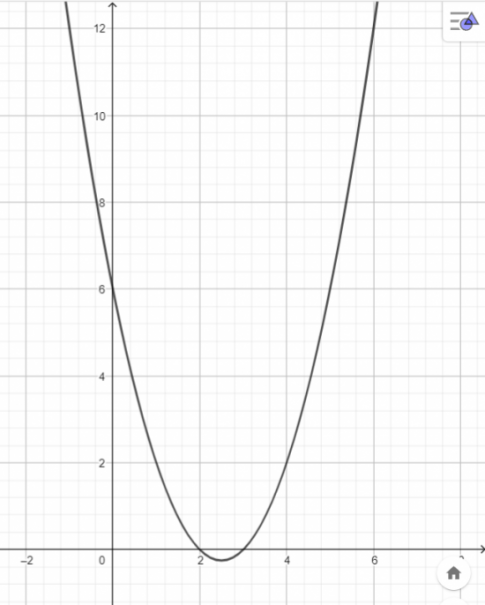
b.
- Hàm số f(x) đồng biến trên khoảng: $\left (\frac{5}{2};+\infty \right)$
- Hàm số f(x) nghịch biến trên khoảng: $\left (-\infty ;\frac{5}{2}; \right)$.
c. $f(x) = 0$ có hai nghiệm là x1 = 2; x2 = 3, nên $f(x)$ $\geq $ 0 $\Leftrightarrow $ x $\geq $ 3 hoặc x $\leq $ 2.
Xem toàn bộ: Giải bài tập ôn tập cuối năm
Giải những bài tập khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận