Giải chi tiết bài tập 5 trang 28 toán 12 chuyên đề cd

Gọi x, y lần lượt là cổ phiếu  A và B:

Ta có hàm mục tiêu:

Theo đề bài, ta có:

Tổng số tiền đầu tư không vượt quá 1,2 tỉ đồng:

Số lượng cổ phiếu B không vượt quá 10 000:

Ta có biểu diễn bài toán quy hoạch tuyến tính như sau:

Ta cần tìm giá trị lớn nhất của biểu thức T =1500x +4800y khi (x,y) thỏa mãn hệ bất phương trình trên.

Bước 1: Xác định miền nghiệm của hệ:

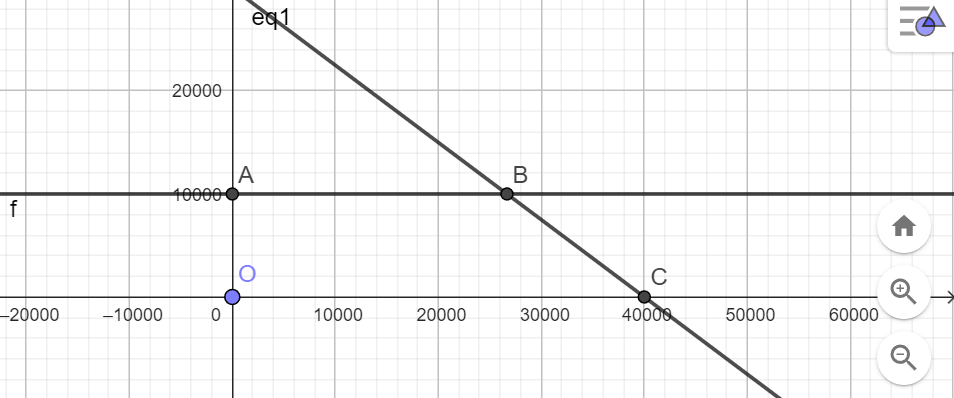
Miền nghiệm là miền OABC với tọa độ các đỉnh: A(0;10000);B(26666,67;10000), C(40000;0), O(0;0)

Bước 2: Tính giá trị biểu thức T tại các đỉnh tứ giác này:

T(0;10000)=48000000 , T(26666,67;10000)= 88000000, T(40000;0)=6000000

Bước 3: So sánh các giá trị vừa tìm được, ta thấy T đạt giá trị lớn nhất tại (x;y)=( 26666,67;10000).

Vậy cần mua 26666 cổ phiếu loại A và 10000 cổ phiếu loại B để có lợi nhuận tối đa.