CHƯƠNG 3. ĐỊNH LÝ PYTHAGORE. CÁC LOẠI TỨ GIÁC THƯỜNG GẶP

BÀI 3. HÌNH THANG – HÌNH THANG CÂN

1. HÌNH THANG, HÌNH THANG CÂN 

HĐKP1:

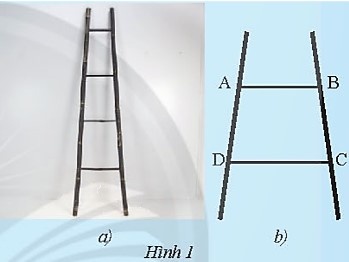
Nhận xét: Hai cạnh AB và CD của tứ giác ABCD song song với nhau.

=> Kết luận: 

Hình thang là tứ giác có hai cạnh đối song song.

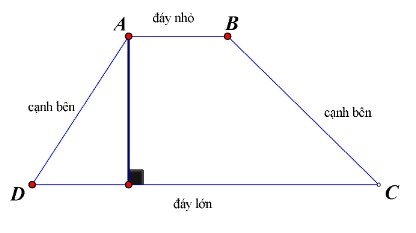
Hình trên là hình thang ABCD với AB // CD. Ta có:

- Các đoạn thẳng AB, CD gọi là các cạnh đáy (hoặc đáy).

Nếu AB < CD thì AB gọi là đáy nhỏ, CD gọi là đáy lớn.

- Các đoạn thẳng AD, BC gọi là các cạnh bên. 

- AH là đường vuông góc kẻ từ A đến đường thẳng CD, đoạn thẳng AH gọi là đường cao của hình thang.

=> Kết luận:

Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

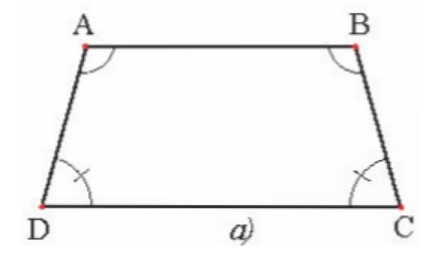
Hình thang cân ABCD với hai đáy là AB và CD (Hình 3a) có A=B; C=D.

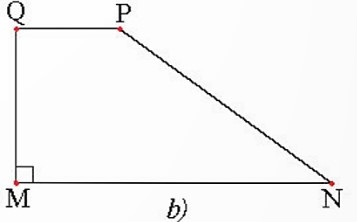
Hình thang có một góc vuông được gọi là hình thang vuông (Hình 3b).

Ví dụ 1: (SGK – tr69)

Thực hành 1:

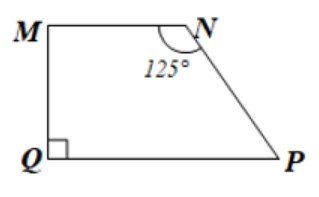
Xét hình thang MNPQ (MN // QP) có

Q=90°

MNPQ là hình thang vuông

M=Q=90°

Áp dụng định lí tổng các góc của một tứ giác, ta có: 

M+N+P+Q=360°

P=360°-(M+N+Q)

Do đó: P=360°-90°+90°+125°=55°

Vậy các góc chưa biết của hình thang MNPQ là: M=90°;P=55°

b)

Xét hình thang MNPQ (MN // QP) có:

P=Q=110°

⇒ MNPQ là hình thang cân.

Suy ra M=N=180°-110°=70°

Vậy các góc chưa biết của hình thang MNPQ là: M=70°;N=70°

Vận dụng 1:

Hình thang cân ABCD có: $D=C=75^{o}$

nênA=B=180°-75°=105° 

Vận dụng 2:

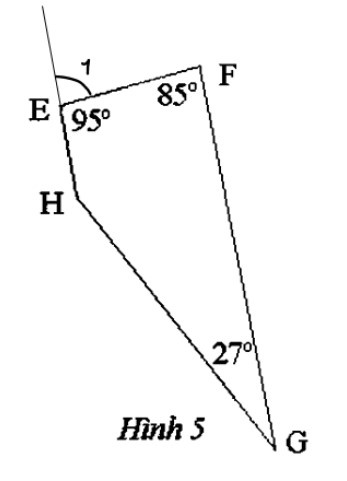
a) Ta có $\widehat{HEF}+\hat{E_{1}}=180$° (hai góc kề bù)

Suy ra $\hat{E_{1}}=180^{o}-\widehat{HEF}$=180°-95°=85°

Do đó $\hat{E_{1}}=\hat{F}$=85°

Mà hai góc này ở vị trí so le trong 

nên HE // GF (DHNB)

Xét tứ giác EFGH có:

 HE // GF 

nên EFGH là hình thang (DHNB)

b) Xét hình thang EFGH có: 

E+F+G+H=360°  (tổng các góc của một tứ giác).

Suy ra H=360° -E+F+G

=360° -(95°+85°+27°)=153°

Vậy góc chưa biết của tứ giác EFGH là H=153°.

2. TÍNH CHẤT CỦA HÌNH THANG CÂN 

HĐKP2.

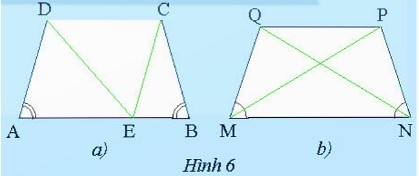
a)

+) Xét hình thang cân ABCD (AB // DC) có A=B

Vì CE // AD nên A=CEB (đồng vị).

Do đó CEB=B

Xét ΔCEB có:

 CEB=B nên là tam giác cân tại C.

+) Do ΔCEB cân tại C (cmt) nên CE = CB       (1)

Xét ΔADE và ΔCED có:

ADE=CED (do AD // CE);

DE là cạnh chung;

DEA=EDC (do DC // AB).

Do đó ΔADE=ΔCED (g.c.g).

Suy ra AD=CE (hai cạnh tương ứng)        (2)

Từ (1) và (2) ta có AD=BC.

b) Vì MNPQ là hình thang cân

suy ra MQ = NP.

Xét hình thang cân MNPQ (MN // QP) có:

 QMN=PNM

Xét ΔMNQ và ΔNMP có:

MQ = NP (cmt);

QMN=PNM (cmt);

MN là cạnh chung.

Do đó ΔMNQ=ΔNMP (c.g.c)

Suy ra NQ = MP (hai cạnh tương ứng).

=> Kết luận:

Trong hình thang cân:

- Hai cạnh bên bằng nhau.

- Hai đường chéo bằng nhau.

Ví dụ 2. (SGK-tr70)

Chú ý:

Nếu một hình thang là hình thang cân thì nó có hai cạnh bên bằng nhau, nhưng một hình thang có hai cạnh bên bằng nhau thì chưa chắc là hình thang cân.

VD:

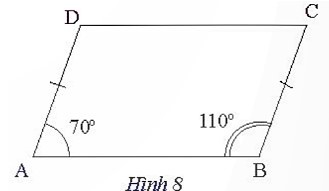
Hình thang ABCD trong hình 8 có hai đáy là: AB, CD và hai cạnh bên bằng nhau AD = BC nhưng không phải hình thang cân (vì hai góc A và B cùng kề một đáy không bằng nhau).

Thực hành 2.

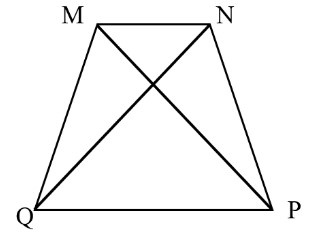
Xét hình thang cân MNPQ (MN // PQ), theo tính chất hình thang cân, ta có:

+ MQ = NP (hình thang cân có hai cạnh bên bằng nhau)

+ MP = NQ (hình thang cân có hai đường chéo bằng nhau).

Vậy các đoạn thẳng bằng nhau trong hình thang cân MNPQ là MQ = NP; MP = NQ.

Vận dụng 3:

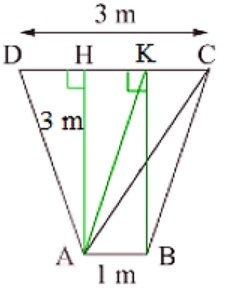
Xét hình thang cân ABCD (AB // DC) có:

D=C

AD = BC

AC = BD (tính chất hình thang cân).

Kẻ BK ⊥ DC.

Ta có AB // DC và BK ⊥ DC

Suy ra BK ⊥ AB 

nên ABK = $90^{o}$

Xét ∆AHK và ∆ABK có:

$\widehat{KHA}=\widehat{ABK}= 90^{o}$;

AK là cạnh chung;

$\widehat{AKH}=\widehat{KAB}$ (vì DC // AB).

Do đó ∆AHK = ∆ABK (cạnh huyền – góc nhọn)

Suy ra HK = BK = 1m (hai cạnh tương ứng).

Xét ∆AHD và ∆BKC có:

$\widehat{AHD}=\widehat{BKC}=90^{o}$;

AD = BC (cmt);

D=C (cmt).

Do đó ΔAHD=ΔBKC (cạnh huyền – góc nhọn).

Suy ra DH=CK (hai cạnh tương ứng).

Mà DH+HK+CK=DC

Hay 2DH=DC–HK

Khi đó DH=CK=$\frac{DC-HK}{2}$ 

=$\frac{3-1}{2}=1$(m) và HC = 2 m.

Áp dụng định lí Pythagore cho ΔAHD vuông tại H, ta có:

$AD^{2} =AH^{2} +DH^{2} =3^{2} +1^{2} =9+1=10$. Do đó $AD=\sqrt{10}$ (m).

Áp dụng định lí Pythagore cho ΔAHCvuông tại H, ta có:

$AC^{2} = AH^{2} + HC^{2} = 3^{2} + 2^{2} = 13$.

Do đó $AC = \sqrt{13}$ (m).

Vậy $AD=BC= \sqrt{10}$ m, $AC=BD=\sqrt{13}$ m.

3. DẤU HIỆU NHẬN BIẾT HÌNH THANG CÂN 

HĐKP 3.

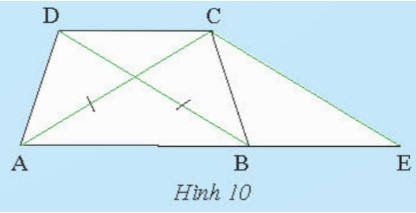
a) Xét hình thang ABCD có:

 AB // CD hay AE // DC nên DCB=EBC (so le trong)

Do DB // CE nên DBC=ECB (so le trong).

Xét ΔDCB và ΔEBC có:

DCB=EBC (cmt);

CB là cạnh chung;

DBC=ECB (cmt).

Do đó ΔDCB=ΔEBC (g.c.g).

Suy ra BD = CE (hai cạnh tương ứng)

Mà AC = BD (gt)

Nên AC = CE.

Xét ΔACE có:

AC = CE 

nên ΔACEcân tại C.

b) Do ΔACE cân tại C (câu a) nên CAE=CEA (hai góc tương ứng).

Mặt khác DB // CE nên DBA=CEA (đồng vị).

Do đó CAE=DBA=CEA

Xét ΔABD và ΔBACcó:

AB là cạnh chung;

DBA=CAB (cmt);

BD = AC (gt).

Do đó ΔABD=ΔBAC (c.g.c).

=> Kết luận:

- Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

- Hình thang có hai đường chéo bằng nhau là hình thang cân.

Ví dụ 3: SGK – tr70

Thực hành 3. 

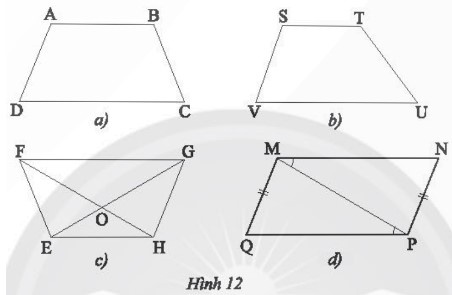
Dùng thước đo góc và thước đo độ dài ta xác định được:

+) Hình 12a) có AB // DC nên tứ giác ABCD là hình thang, ta đo được ADC=BCDnên hình thang ABCD là hình thang cân.

+) Hình 12b) có ST // VU nên tứ giác STUV là hình thang, ta đo được 

 nên hình thang STUV không phải là hình thang cân.

+) Hình 12c) có EH // FG nên tứ giác EFGH là hình thang, ta đo được EG = HF nên hình thang EFGH là hình thang cân.

+) Hình 12d) có:

 MN // QP (do có cặp góc so le trong bằng nhau $\widehat{NMP}=\widehat{MPQ}$ nên tứ giác MNPQ là hình thang, ta đo được:

$\widehat{MQP} \neq \widehat{NPQ}$ nên hình thang MNPQ không phải là hình thang cân.

Vận dụng 4. 

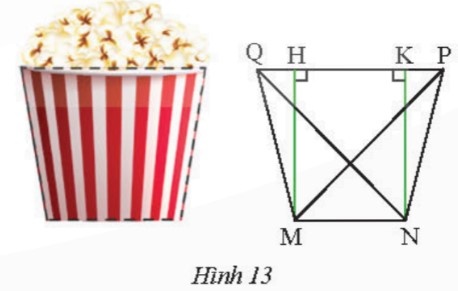
+) MNPQ là hình thang cân nên: 

{MN // QP MQ = NP MQP=NPQ (tính chất hình thang cân)

+) Ta có: MN // QP (cmt) và NKQP (gt)

Suy ra NK⊥MN hay MNK=90°.

Xét ΔMHK và ΔKNM có:

MHK=KNM=90°

MK là cạnh huyền chung;

MKH=KMN (do QP // MN).

Do đó ΔMHK=ΔKNM (cạnh huyền – góc nhọn)

Suy ra HK = NM = 6 cm (hai cạnh tương ứng).

+) Xét ΔMHQ và ΔNKP có:

MHQ=NKP=90°

MQ=NP (cmt);

MQH=NPK (cmt).

Do đó ΔMHQ=ΔNKP (cạnh huyền – góc nhọn).

Suy ra QH=PK (hai cạnh tương ứng).

Mà QH+HK+PK=QP

Hay 2QH=QP–HK

Khi đó 

$QH=PK=\frac{QP-HK}{2}=\frac{10-6}{2}=2$ cm  

Nên HP=HK+KP=6+2=8cm.

+) Áp dụng định lí Pythagore vào DMHP vuông tại H, ta có:

$MP^{2} = MH^{2} + HP^{2}$

Suy ra $MH^{2} = MP^{2}-HP^{2}$

=$8\sqrt{2}^{2}-8^{2}$=64

Do đó MH = 8 cm.

Áp dụng định lí Pythagore vào ΔMHQ vuông tại H, ta có:

$MQ^{2} =MH^{2} +HQ^{2} =8^{2} +2^{2} =64+4=68$

Suy ra $MQ=2\sqrt{17}$ (cm).

Vậy hình thang cân MNPQ có độ dài đường cao là MH=NK=8 cm; độ dài cạnh bên là $2\sqrt{17}$ cm.