CHƯƠNG 1. BIỂU THỨC ĐẠI SỐ

BÀI 3. HẰNG ĐẲNG THỨC ĐÁNG NHỚ

1. BÌNH PHƯƠNG CỦA MỘT TỔNG, HIỆU

HĐKP1:

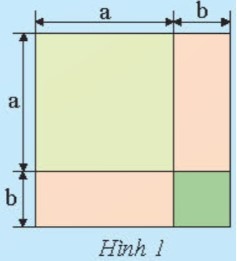
a) Ta xét các cách tính diện tích của các phần tô màu trong Hình 1 như sau:

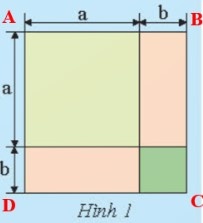
Cách 1: Tính diện tích của hình vuông được ghép bởi 4 hình:

+ Cạnh của hình vuông ABCD được tạo thành là: a + b.

+ Diện tích S của các phần tô màu chính là diện tích của hình vuông ABCD, và bằng:

$S = (a + b)^{2}$ .

Do đó kết quả của bạn An là đúng.

Cách 2: Tính diện tích mỗi hình:

+ Diện tích hình vuông màu vàng AEHG là: $a^{2}$.

+  Diện tích hình vuông màu xanh HICK là: $b^{2}$.

+ Diện tích hình chữ nhật màu hồng EBIH là: ab.

+ Diện tích hình chữ nhật màu hồng GHKD là: ba.

+ Diện tích S của các phần tô màu là: 

$a^{2} + b^{2} + ab + ba$.

Do đó kết quả của bạn Mai là đúng.

Cách 3: Tính tổng diện tích hai hình chữ nhật ABIG và GICD (hình vẽ dưới đây).

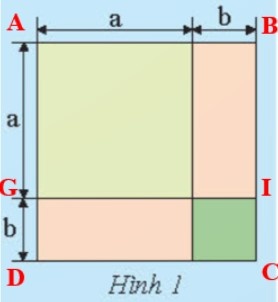
+ Diện tích hình chữ nhật ABIG là: 

$a.(a + b) = a.a + a.b = a^{2} + ab$.

+ Diện tích hình chữ nhật GICD là: 

$(a + b).b = a.b + b.b = ab + b^{2}$.

+ Diện tích S của các phần tô màu là: 

$a^{2} + ab + ab + b^{2} = a^{2} + 2ab + b^{2}$.

Vậy kết quả của bạn Bình là đúng.

=> Kết luận:

- Nếu hai biểu thức P và Q nhận giá trị như nhau và mọi giá trị của biến thì ta nói P = Q là một đồng nhất thức hay hằng đẳng thức.

- Với hai biểu thức tuỳ ý A và B, ta có:

$(A+B)^{2} =  A^{2} + 2AB + B^{2}$

$(A - B)^{2} = A^{2}- 2AB + B^{2}$

Ví dụ 1: (SGK – tr19)

Ví dụ 2: (SGK – tr19)

Ví dụ 3: (SGK – tr19)

Thực hành 1:

a) $(3x + 1)^{2}$

$= (3x)^{2} + 2.3x.1 + 1^{2}$

$= 9x^{2} + 6x + 1$.

b) $(4x + 5y)^{2}$

$= (4x)^{2} + 2.4x.5y + (5y)^{2}$

$= 16x^{2} + 40xy + 25y^{2}$.

c) $(5x-\frac{1}{2})^{2}=5x^{2}+2.5.x.\frac{1}{2}+(\frac{1}{2})^{2}$

$=25^{2}+5.x+\frac{1}{4}$ 

d) $(-x + 2y^{2})^{2}$

$= (-x)^{2} + 2.(-x).2y^{2} + (2y^{2})^{2}$

$= x^{2}-4xy^{2} + 4y^{4}$.

Thực hành 2:

a) $a^{2} + 10ab + 25b^{2}$

$= a^{2} + 2.a.5b + (5b)^{2}$

$= (a + 5b)^{2}$.

b) $1 + 9a^{2}-6a$

$= 1 - 6a + 9a^{2}$

$= 1^{2} - 2.1.3a + (3a)^{2}$

$= (1 -3a)^{2}$.

Hoặc ta có thể viết như sau:

$1 + 9a^{2}- 6a$

$= 9a^{2}-6a + 1$

$= (3a)^{2}-2.3a.1 + 1^{2}$

$= (3a -1)^{2}$.

Thực hành 3.

a) $52^{2} = (50 + 2)^{2} = 50^{2} + 2.50.2 + 2^{2}$ 

= $2500 + 200 + 4 = 2704$.

b) $98^{2} = (100 -2)^{2} = 100^{2}-2.100.2 + 2^{2}$ 

= $10 000 -400 + 4 = 9 604$.

Vận dụng 1.

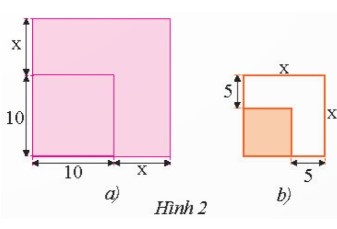
a) Mảnh vườn hình vuông có cạnh 10 m được mở rộng cả hai cạnh thêm x (m) nên mảnh vườn lúc này có dạng hình vuông với độ dài cạnh là 10 + x (m).

Diện tích mảnh vườn sau khi mở rộng là:

$(10 + x)^{2} = 10^{2} + 2.10.x + x^{2}$ 

$= 100 + 20x + x^{2} (m^{2})$.

Vậy biểu thức biểu thị diện tích mảnh vườn sau khi mở rộng là $100 + 20x + x^{2} (m^{2})$.

b) Mảnh vườn hình vuông trước khi mở rộng có độ dài cạnh là: x - 5 (m).

Diện tích mảnh vườn hình vuông trước khi mở rộng là:

$(x-5)^{2}=x^{2}-2.x.5 + 5^{2} = x^{2}-10x + 25 (m^{2})$.

Vậy biểu thức biểu thị diện tích mảnh vườn trước khi mở rộng là $x^{2}-10x + 25 (m^{2})$.

2. HIỆU CỦA HAI BÌNH PHƯƠNG 

HĐKP2.

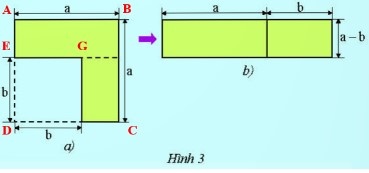
+ Diện tích hình vuông ABCD là: $a^{2}$.

+ Diện tích hình vuông EGHD là: $b^{2}$.

+ Diện tích phần tô màu ở Hình 3a là: $a^{2}-b^{2}$.

+ Chiều dài của hình chữ nhật trong Hình 3b là: a + b.

+ Chiều rộng của hình chữ nhật trong Hình 3b là: a – b.

+ Diện tích hình chữ nhật (phần tô màu) trong Hình 3b là: (a + b)(a – b).

b) Ta có:

$(a + b)(a - b) = a.(a - b) + b.(a -b) = a.a - ab + ba - b.b = a^{2}-b^{2}$.

Vậy hai hình trên có diện tích bằng nhau.

=> Kết luận:

Với hai biểu thức tuỳ ý A và B, ta có:

$A^{2}- B^{2} = (A + B). (A - B)$

Ví dụ 4. (SGK-tr20)

Ví dụ 5 (SGK-tr20)

Thực hành 4.

a) $(4 - x).(4 + x) = 4^{2}-x^{2} = 16 - x^{2}$.

b) $(2y + 7z).(2y - 7z) = (2y)^{2}-(7z)^{2} = 4y^{2}-49z^{2}$.

c) $(x + 2y^{2}).(x-2y^{2}) = x^{2}-(2y^{2})^{2} = x^{2}-4y^{4}$.

Thực hành 5.

a) $82 . 78 = (80 + 2).(80 - 2) = 80^{2}- 2^{2} = 6 400 - 4 = 6 396$.

b) $87 . 93 = (90 - 3).(90 + 3) = 90^{2}-3^{2} = 8 100 - 9 = 8 091$.

c) $125^{2} -25^{2} = (125 + 25).(125- 25) = 150 . 100 = 15 000$.

Vận dụng 2.

$65^{2}-35^{2}=(65 + 35) . (65-35) = 100 . 30 = 3 000$.

$102 . 98 = (100 + 2) . (100 - 2) = 100^{2}-2^{2} = 10 000 - 4 = 9 996$.

3. LẬP PHƯƠNG CỦA MỘT TỔNG, MỘT HIỆU

HĐKP 3.

$(a + b)^{3} = (a + b)(a + b)^{2}$

$= (a + b)(a^{2} + 2ab + b^{2})$

$= a(a^{2} + 2ab + b^{2}) + b(a^{2} + 2ab + b^{2})$

$= a.a^{2} + a.2ab + a.b^{2} + b.a^{2} + b.2ab + b.b^{2}$

$= a^{3} + 2a^{2}b + ab^{2} + a^{2}b + 2ab^{2} + b^{3}$

$= a^{3} + (2a^{2}b + a^{2}b) + (ab^{2} + 2ab^{2}) + b^{3}$

$= a^{3} + 3a^{2}b + 3ab^{2} + b^{3}$.

$(a - b)^{3} = (a - b)(a - b)^{2}$

$= (a - b)(a^{2}- 2ab + b^{2})$

$= a(a^{2}-2ab + b^{2})-b(a^{2}-2ab + b^{2})$

$= a.a^{2}-a.2ab + a.b^{2} -b.a^{2} + b.2ab - b.b^{2}$

$= a^{3}-2a^{2}b + ab^{2}-a^{2}b + 2ab^{2}-b^{3}$

$= a^{3}- (2a^{2}b + a^{2}b) + (ab^{2} + 2ab^{2})-b^{3}$

$= a^{3}-3a^{2}b + 3ab^{2}-b^{3}$.

=> Kết luận:

Với hai biểu thức tuỳ ý A và B, ta có:

$(A+B)^{3}=A^{3}+3A^{2}B+3AB^{2}+B^{3}$

$(A-B)^{3}=A^{3}-3A^{2}B+3AB^{2}-B^{3}$

Ví dụ 6: SGK – tr21

Thực hành 6. 

a) $(x + 2y)^{3}$

$= x^{3} + 3.x^{2}.2y + 3.x.(2y)^{2} + (2y)^{3}$

$= x^{3} + 6x^{2}y + 12xy^{2} + 8y^{3}$.

b) $(3y - 1)^{3}$

$= (3y)^{3}-3.(3y)^{2}.1 + 3.3y.1^{2}-1^{3}$

$= 27y^{3}-27y^{2} + 9y-1$.

Vận dụng 3. 

Phần lòng trong của thùng chứa có dạng hình lập phương với độ dài cạnh là:

x – 3 – 3 = x – 6 (cm).

Thể tích phần lòng trong của thùng là:

$(x-6)^{3} = x^{3}-3.x^{2}.6 + 3.x.6^{2}-6^{3}$

             = $x^{3}-18x^{2} + 108x-216 (cm^{3})$.

Vậy dung tích (sức chứa) của thùng là $x^{3}-18x^{2} + 108x -216 (cm^{3})$.