CHƯƠNG 1. BIỂU THỨC ĐẠI SỐ

BÀI 2. CÁC PHÉP TOÁN VỚI ĐA THỨC NHIỀU BIẾN

1. CỘNG, TRỪ HAI ĐA THỨC.

HĐKP1:

Số tiền lần 1, lần 2 lần lượt là:

$P_{1}=2x^{2}a+4xa+5xya$ (đồng)

$P_{2}=4x^{2}a+3xa+6xya$ (đồng)

a) Tổng số tiền của hai lần là: 

$T = P_{1} + P_{2} = 6x^{2}a + 7xa + 11xya$ (đồng)

b) Chênh lệch số tiền giữa lần 2 và lần 1 là:

$H = P_{2} - P_{1} = 2x^{2}a - xa + xya$ (đồng)

=> Kết luận:

Muốn cộng hay trừ hai đa thức ta làm như sau:

- Viết hai đa thức trong ngoặc và nối với nhau bằng dấu (+) hay trừ (-).

- Bỏ dấu ngoặc rồi thu gọn đa thức thu được.

Ví dụ 1: (SGK – tr13)

Thực hành 1:

M + N = 1 + x + 2xy;

M - N = 1 – x + 4xy - $4x^{2}y^{2}$

2. NHÂN HAI ĐA THỨC 

• Nhân hai đơn thức

HĐKP2.

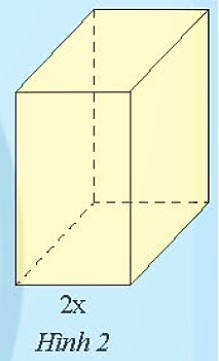
Chiều dài và chiều cao đều bằng k.2x = 2kx.

a) Diện tích đáy: $S = 2x.2kx = 4kx^{2} (cm^{2})$

b) Thể tích: $V = 2x.2kx.2kx = 8k^{2}x^{3} (cm^{3})$

=> Để nhân hai đơn thức, ta nhân các hệ số với nhau, nhân các luỹ thừa cùng biến, rồi nhân các kết quả đó với nhau.

Ví dụ 2: SGK – tr14

Thực hành 2. 

a) $(4x^{3}).(-6x^{3}y) = -24x^{6}y$

b) $(-2y).(-5xy^{2}) = 10xy^{3}$

c) $(-2a)^{3}.(2ab)^{2} = -32a^{5}b^{2}$

• Nhân hai đa thức:

HĐKP 3:

a) Cách 1: 

$S = 2x.y + 2x.3x + 2x.2 = 2xy + 6x^{2} + 4x (m^{2})$ (tính diện tích từng phòng rồi cộng lại).

Cách 2:

$S = 2x.(y + 3x + 2)  = 2xy + 6x^{2} + 4x (m^{2})$ (tính tổng độ dài một chiều của căn hộ, rồi nhân với chiều kia).

b) $S' = 2xy + 6x2  + 7x + y + 2 (m^{2})$

=> Kết luận:

- Để nhân đơn thức với đa thức, ta nhân đơn thức đó với từng hạng tử của đa thức, rồi cộng các kết quả với nhau.

- Để nhân hai đa thức, ta nhân từng hạng tử của đa thức này với đa thức kia, rồi cộng các kết quả với nhau.

Ví dụ 3 (SGK-tr15)

Thực hành 3. 

a) $(-5a^{4}).(a^{2}b -ab^{2}) = -5a^{6}b + 5a^{5}b^{2}$

b) $(x+2y).(xy^{2}- 2y^{3}) =  x^{2}y^{2}-4y^{4}$.

Vận dụng 1. 

+ Quãng đường thuyền đi được: S = (v+3).t = vt + 3t (km)

+ Quãng đường ca nô đi được: S' = (2v-3).t = 2vt – 3t (km).

+ Khoảng cách giữa hai phương tiện d = S + S'= (vt+3t) + (2vt – 3t) = 3vt (km).

Vận dụng 2:

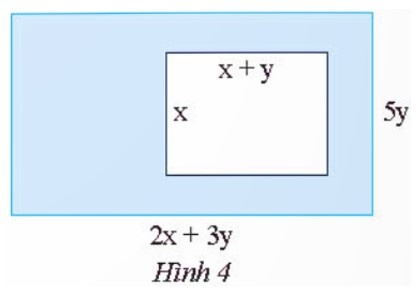
$S= (2x+3y) .5y- x.(x+y) = 9xy + 15y^{2}-x^{2}$

3. CHIA ĐA THỨC CHO ĐƠN THỨC

• Chia đơn thức cho đơn thức.

HĐKP 4.

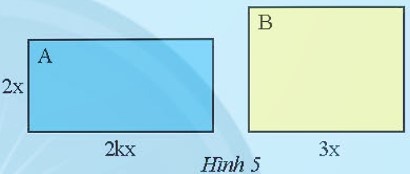
Diện tích của A là:

$S = 2x.2kx = 4kx^{2} (cm^{2})$

Chiều rộng của B là: 

$\frac{S}{3x}=\frac{4kx^{2}}{3x}=\frac{4}{3}kx(cm)$

=> Kết luận:

Muốn chia đơn thức A cho đơn thức B (với A chia hết cho B), ta làm như sau:

- Chia hệ số của A cho hệ số của B.

- Chia luỹ thừa của từng biến trong A cho luỹ thừa của cùng biến đó trong B.

- Nhân các kết quả tìm được với nhau.

Ví dụ 4: SGK – tr15

Thực hành 4. 

$8x^{4}y^{5}z^{3}: 2x^{3}y^{4}z = 4xyz^{2}$

Vận dụng 3. 

$B = 12x^{2}y : (3y) = 4x^{2}$

• Chia đa thức cho đơn thức

HĐKP5. 

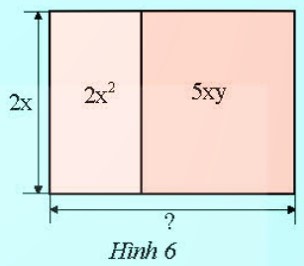
a) Chiều rộng hai tấm giấy lần lượt là $2x^{2} : (2x) = x$ (m) và $5xy : (2x) = \frac{5}{2}y$ (m).

Chiều rộng của bức tường là:

$x + \frac{5}{2}y$ (m)

b) Chiều rộng của bức tường cũng bằng diện tích của bức tường chia cho chiều cao, tức là bằng $(2x^{2} + 5xy) : (2x)$. 

Do đó, $(2x^{2} + 5xy) : (2x) = x + \frac{5}{2}y$ (m)

=> Kết luận:

Muốn chia một đa thức cho một đơn thức (trường hợp chia hết), ta chia từng hạng tử của đa thức cho đơn thức đó, rồi cộng các kết quả tìm được với nhau.

Ví dụ 5: SGK – tr16

Thực hành 5: 

a) $(5ab - 2a^{2}) : a = 5b - 2a$

b) $(6x^{2}y^{2}-xy^{2} + 3x^{2}y) : (-3xy)$ 

$= -2xy + \frac{1}{3}y-x$

Vận dụng 4.  

$h = V : S = (6x^{2}y-8xy^{2}) : (2xy) = 3x - 4y$