1. ĐƠN THỨC MỘT BIẾN

• Sơ lược về đơn thức một biến:

- Đơn thức một biến (đơn thức) là BTĐS có dạng tích của môt số thực với một lũy thừa của biến, trong đó số thực gọi là hệ số, số mũ của lũy thừa của biến gọi là bậc của đơn thức. 

VD:

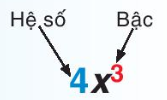
+ Biểu thức 4x$^{3}$ là một đơn thức, trong đó 4 là hệ số, số mũ 3 của x là bậc của đơn thức đó.

+ Đơn thức -0,5x có hệ số là -0,5 và có bậc là 1 (vì x = x$^{1}$).

+ Một số khác 0 là một đơn thức bậc 0.

* Chú ý: Số 0 cũng được là một đơn thức. Đơn thức này không có bậc.

?.

a) 2x$^{6}$

• Hệ số: 2

• Bậc: 6

b) $\frac{-1}{5}x^{2}$

• Hệ số: $\frac{-1}{5}$

• Bậc: 2

c) -8

• Hệ số: -8

• Bậc: 0

d) 3$^{2}$x

• Hệ số: 3$^{2}$

• Bậc: 1

- Với các đơn thức một biến, ta có thể:

+ Cộng (hay trừ) hai đơn thức cùng bậc bằng cách cộng (hay trừ) các hệ số với nhau và giữ nguyên lũy thừa của biến. Tổng nhận được là một đơn thức. 

VD: 

$-3x^{4} + x^{4} = (-3+1).x^{4} = -2x^{4}$

$3,7x^{2} – 1,2x^{2} = (3,7 -1,2).x^{2} = 2,5x^{2}$

+ Nhân hai đơn thức tùy ý bằng cách nhân hai hệ số với nhau và nhân hai lũy thừa của biến với nhau. Tích nhận được cũng là một đơn thức.

VD: 

$(0,5x).(6x^{2}) = (0,5.6). (x.x^{2}) = 3x^{3}$

$(-6x^{3}).(\frac{2}{3}x^{2})= (-6). \frac{2}{3}(x^{3}.x^{2}) = -4x^{5}$

?.

Đơn thức bậc 3.

Luyện tập 1:

a) $5x^{3}+x^{3}=(5+1)x^{3}=6x^{3}$

b) $\frac{7}{4}x^{5}-\frac{3}{4}x^{5}=(\frac{7}{4}+\frac{3}{4})x^{5}=\frac{5}{2}x^{5}$

c) $(-0,25x^{2}).(8x^{3})$

=$(-0,25.8)(x^{2}.x^{3})$

=-2x$^{5}$

2. KHÁI NIỆM ĐA THỨC MỘT BIẾN

-  Đa thức một biến (đa thức) là tổng của những đơn thức cùng một biến; mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.

- Số 0 cũng được coi là một đa thức, gọi là đa thức không.

* Chú ý: 

- Một đơn thức cũng là một đa thức.

- Ta thường kí hiệu đa thức bằng một chữ cái in hoa. Đôi khi còn viết thêm kí hiệu biến trong ngoặc đơn.

VD: 

A = A(x) = $6x^{3} -5x^{2} -4x^{3} + 7$

?.

Mỗi số thực là một đơn thức, mà một đơn thức cũng là một đa thức nên mỗi số thực là một đa thức.

Ví dụ 1: SGK-tr26

Luyện tập 2:

Đa thức B có 4 hạng tử: $2x^{4}; -3x^{2}; x$ và 1.

3. ĐA THỨC MỘT BIẾN THU GỌN

-  Đa thức thu gọn: Là các đa thức không chứa hai đơn thức nào cùng bậc.

Ví dụ 2: SGK-tr27

Luyện tập 3:

* Chú ý: 

- Một đơn thức cũng là một đa thức.

- Ta thường kí hiệu đa thức bằng một chữ cái in hoa. Đôi khi còn viết thêm kí hiệu biến trong ngoặc đơn.

VD: 

$A = A(x) = 6x^{3} -5x^{2} -4x^{3} + 7$

?.

Mỗi số thực là một đơn thức, mà một đơn thức cũng là một đa thức nên mỗi số thực là một đa thức.

Ví dụ 1: SGK-tr26

Luyện tập 3:

$P = 2x^{3}-5x^{2}+4x^{3}+4x+9+x$

$ = (2x^{3}+4x^{3}) -5x^{2}+(4x+x)+9$

$ = 6x^{3}-5x^{2}+5x+9$

4. SẮP XẾP ĐA THỨC MỘT BIẾN

• Sắp xếp đa thức theo lũy thừa giảm của biến:

Xét các đa thức khác đa thức không:

- Để thuận lợi cho việc tính toan các đa thức một biến, người ta thường viết chúng dưới dạng thu gọn và sắp xếp các hạng tử của nó theo lũy thừa giảm của biến.

VD: Sắp xếp các hạng tử của đa thức 

P = 5x$^{2}$ -2x + 1 – 3x$^{4}$ theo lũy thừa giảm của biến, ta được P = -3x$^{4}$ + 5x$^{2}$ -2x + 1.

- Trong đa thức P, ta thấy có các đơn thức bậc 4 và bậc 2, nhưng khuyết đơn thức bậc 3. Tuy nhiên khi cần, ta cũng có thể viết:

$P = -3x^{4} + 0x^{3} + 5x^{2} – 2x + 1$.

Ở đây, ta coi rằng hệ số của lũy thừa bậc 3 là 0.

Luyện tập 4:

a) $A=3x-4x^{4}+x^{3}$

      $=-4x^{4}+x^{3}+3x$

b) $B=-2x^{3}-5x^{2}+2x^{3}+4x+x^{2}-5$  

$ =(-2x^{3}+2x^{3})+(-5x^{2}+x^{2})+x-5$

$ =-4x^{2}+4x-5$

c) $C=x^{5}-\frac{1}{2}x^{3}+\frac{3}{4}x-x^{5}+6x^{2}-2$

$=(x^{5}-x^{5})-\frac{1}{2}x^{3}+6x^{2} +\frac{3}{4} $

$=\frac{1}{2}x^{3}+6x^{2} +\frac{3}{4}x-2$  

* Chú ý:

Người ta cũng có thể sắp xếp đa thức theo lũy thừa tăng của biến.

VD: Ta có thể sắp xếp các hạng tử của đa thức P trên đây như sau:

$P = 1 - 2x + 5x^{2} - 3x^{4}$

5. BẬC VÀ CÁC HỆ SỐ CỦA MỘT ĐA THỨC

• Bậc, hệ số cao nhất và hệ số tự do của một đa thức

HĐ1.

Bậc của hạng tử -3x$^{4}$ là 4.

Bậc của hạng tử 5x$^{2}$ là 2.

Bậc của hạng tử 2x là 1.

Bậc của hạng tử 1 là 0.

HĐ2.

Trong P, hạng tử -3x$^{4}$ có bậc cao nhất.

⇒ Hạng tử -3x$^{4}$ có hệ số là –3 và bậc là 4.

HĐ3.

Trong P, hạng tử 1 có bậc là 0.

=> Kết luận:

Trong một đa thức thu gọn và khác đa thức không.

+ Bậc của hạng tử có bậc cao nhất gọi là bậc của đa thức đó.

+ Hệ số của hạng tử có bậc cao nhất gọi là hệ số cao nhất của đa thức đó.

+ Hệ số của hạng tử bậc 0 gọi hệ số tự do của đa thức đó.

* Chú ý:

- Đa thức không là đa thức không có bậc.

- Trong một đa thức thu gọn, hệ số cao nhất phải khác 0 (các hệ số khác có thể bằng 0).

- Muốn tìm bậc của một đa thức chưa thu gọn, ta phải thu gọn đa thức đó.

?. 

- Một số khác 0 cũng là một đa thức. Bậc của nó bằng 0.

Ví dụ 3: SGK-tr28

Luyện tập 5:

a) $5x^{2}-2x+1-3x^{4}$

- Hạng tử có bậc cao nhất là -3x$^{4}$, bậc của nó là 4, hệ số là -3

- Hệ số tự do là 1.

b) $1,5x^{2}-3,4x^{4}+0,5x^{2}-1$.

- Hạng tử có bậc cao nhất là -3,4x$^{4}$, bậc của nó là 4, hệ số là -3,4

- Hệ số tự do là -1.

6. NGHIỆM CỦA ĐA THỨC MỘT BIẾN

• Giá trị và nghiệm của một đa thức

HĐ4.

• G(-2)=(-2)$^{2}$ -4=0 

• G(-1)=(-1)$^{2}$-4=-3 

• G(0)=(0)$^{2}$-4=-4 

• G(1)=(1)$^{2}$-4=-3 

• G(2)=(2)$^{2}$-4=0 

HĐ5.

Theo hoạt động 1, với giá trị x=2 và x=-2 thì G(x)=0.

=> Kết luận:

Nếu tại x = a, đa thức F(x) có giá trị bằng 0, tức là F(a) = 0, tức F(a) = 0, thì ta gọi a (hoặc x = a) là một nghiệm của đa thức F(x).

Ví dụ 4: SGK -tr 29

Luyện tập 6.

1. Tính giá trị:

F(-1) = 3; F(0) = -2; F(1)= - 3; ; F(2)=0

Một nghiệm của đa thức F(x) là 2.

2. Tìm nghiệm của đa thức E(x)=x$^{2}$+x.

E(0)=0$^{2}$ + 0

⇒ Nghiệm của đa thức E(x) là 0

Vận dụng.

a) Trong đa thức H(x), hạng tử -5x$^{2}$ có bậc cao nhất.

=> Hạng tử -3x$^{4}$ có hệ số là –5 và bậc là 2.

- Hệ số tự do trong đa thức H(x) là 0.

b) x=0 là một nghiệm của đa thức H(x) vì tại x=0, đa thức ta được giá trị của H(x) bằng 0.

Kết quả đó nói lên: 0 là một nghiệm của đa thức H(x) => H(0)=0.

c) H(1)=-5.1$^{2}$+15.1=10

    H(2)=-5.2$^{2}$+15.2=10

    H(3)=-5.3$^{2}$+15.3=0

=> Kết luận:

- Khi ném vật từ một điểm trên mặt đất sau thời gian là 1 giây, thì độ cao của vật là 10m.

- Khi ném vật từ một điểm trên mặt đất sau thời gian là 2 giây, thì độ cao của vật là 10m.

- Khi ném vật từ một điểm trên mặt đất sau thời gian là 3 giây, thì vật rơi trở lại mặt đất (0m).