CHƯƠNG 4:  GÓC VÀ ĐƯỜNG THẲNG SONG SONG

BÀI 2. TIA PHÂN GIÁC

1. TIA PHÂN GIÁC CỦA MỘT GÓC 

HĐKP1:

Theo em, tia Oz chia $\widehat{xOy}$ thành hai góc bằng nhau.

Kết luận:

Tia phân giác của một góc là tia xuất phát từ đỉnh của góc, đi qua một điểm trong của góc và tạo với hai cạnh của góc đó là hai góc bằng nhau.

Thực hành 1: 

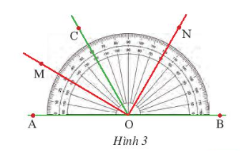
Ta thấy:

• Tia OM là tia phân giác của góc $\widehat{AOC}$ (vì điểm M nằm trong góc $\widehat{AOC}$ và $\widehat{AOM}$ = $\widehat{MOC}$ = 30$^{\circ}$).

• Tia OM là tia phân giác của góc $\widehat{BOC}$ (vì điểm M nằm trong góc $\widehat{BOC}$ và $\widehat{BON}$ = $\widehat{NOC}$ = 60$^{\circ}$).

Vận dụng 1:

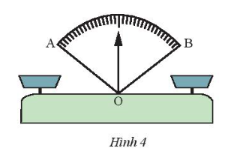
Khi cân thăng bằng thì kim là tia phân giác của $\widehat{AOB}$

2. CÁCH VẼ TIA PHÂN GIÁC

HĐKP2:

Vì tia Oz là tia phân giác của $\widehat{xOy}$ 

$\widehat{xOz}$ = $\widehat{yOz}$ và $\widehat{xOy}$= $\widehat{xOz}$ + $\widehat{zOy}$

$\widehat{xOy}$ =$\widehat{xOz}$ = 32$^{\circ}$

$\widehat{xOy}$ =$\widehat{xOz}$ + $\widehat{zOy}$ = 32$^{\circ}$ + 32$^{\circ}$ = 64$^{\circ}$.

Thực hành 2:

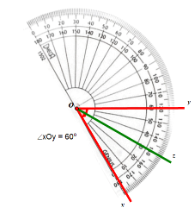
• Vẽ $\widehat{xOy}$ = 60$^{\circ}$. Có $\widehat{xOz}$ = $\widehat{zOy}$ và $\widehat{xOy}$ = $\widehat{xOz}$ + $\widehat{zOy}$

$\widehat{xOz}$=$\frac{60^{\circ}}{2}$=30$^{\circ}$

• Dùng thước đo góc vẽ tia Oz đi qua một điểm trong của $\widehat{xOy}$ sao cho $\widehat{xOz}$ = 30$^{\circ}$

Ta được tia Oz là tia phân giác của $\widehat{xOy}$

Vận dụng 2. 

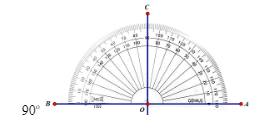
• Vẽ góc bẹt $\widehat{AOB}$.  Ta có:$\widehat{AOC}$ =$\widehat{COB}$ và $\widehat{AOB}$ = $\widehat{AOC}$ + $\widehat{COB}$

$\widehat{AOC}$ = 90$^{\circ}$.

• Dùng thước đo góc vẽ tia OC đi qua điểm C nằm trong $\widehat{AOB}$ sao cho $\widehat{AOC}$ = 90$^{\circ}$

• 

Chú ý:

Ta gọi đường thẳng chứa tia phân giác của một góc là đường phân giác của góc đó.

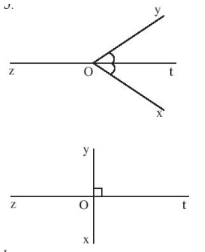
Đường thẳng zt là đường phân giác của $\widehat{xOy}$.