CHƯƠNG 4:  GÓC VÀ ĐƯỜNG THẲNG SONG SONG

BÀI 1. CÁC GÓC Ở VỊ TRÍ ĐẶC BIỆT

1. HAI GÓC KỀ BÙ 

HĐKP1:

a) Hai góc $\widehat{xOy}$ và $\widehat{yOz}$ có cạnh Oy chung, không có điểm trong chung.

b) Có: 

$\widehat{xOy}$ = 30$^{\circ}$ ; $\widehat{yOz}$ = 45$^{\circ}$ ; $\widehat{xOz}$ = 75$^{\circ}$

$\widehat{xOy}$+$\widehat{yOz}$=$\widehat{xOz}$

c) Có:

=> $\widehat{mOn}$+$\widehat{nOp}$=33$^{\circ}$+147$^{\circ}$=180$^{\circ}$

Kết luận:

Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.

Hai góc bù nhau là hai góc có tổng số đo bằng 180$^{\circ}$.

Hai góc vừa kề nhau, vừa bù nhau gọi là hai góc kề bù.

Chú ý:

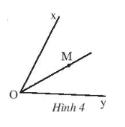
Nếu M là điểm trong của góc xOy thì $\widehat{xOM}$+$\widehat{MOy}$=$\widehat{xOy}$.

Thực hành 1: 

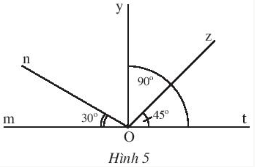
a) Các góc kề với $\widehat{tOz}$ là:  $\widehat{zOn}$; $\widehat{zOy}$;  $\widehat{zOm}$

b) Vì $\widehat{mOn}$= 30$^{\circ}$ => Số đo của góc kề bù với $\widehat{mOn}$ là: 180$^{\circ}$ - 30$^{\circ}$= 150$^{\circ}$

c) Ta có: 

$\widehat{mOn}$+ $\widehat{nOy}$ + $\widehat{yOt}$ = 180$^{\circ}$ =>30$^{\circ}$+$\widehat{nOy}$ + 90$^{\circ}$ = 180$^{\circ}$ => $\widehat{nOy}$ = 180$^{\circ}$ - 30$^{\circ}$ - 90$^{\circ}$ = 60$^{\circ}$

Vậy $\widehat{nOy}$ = 90$^{\circ}$

d) Có: $\widehat{tOz}$ = 45$^{\circ}$

Góc kề bù với $\widehat{tOz}$ có số đo là: 180$^{\circ}$ - 45$^{\circ}$= 135$^{\circ}$

Vận dụng 1:

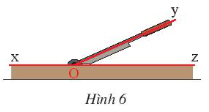
2 góc kề bù trong hình là  $\widehat{xOy}$ và  $\widehat{yOz}$.

2. HAI GÓC ĐỐI ĐỈNH

HĐKP2:

$\widehat{O_{1}}$ có cạnh Ox và Ot, đỉnh O

$\widehat{O_{3}}$ có cạnh Oy và Oz, đỉnh O

Ta có: $\widehat{O_{1}}$ và $\widehat{O_{3}}$ có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.

$\widehat{O_{1}}$ và $\widehat{O_{3}}$ có chung đỉnh.

⇒ Kết luận:

Hai góc đối đỉnh là hai  góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

Chú ý:

Khi $\widehat{O_{1}}$ và $\widehat{O_{3}}$ là hai góc đối đỉnh, ta còn nói: $\widehat{O_{1}}$ đối đỉnh với $\widehat{O_{3}}$;$\widehat{O_{3}}$ đối đỉnh với $\widehat{O_{1}}$; $\widehat{O_{1}}$ và $\widehat{O_{3}}$ đối đỉnh với nhau.

Thực hành 2:

a) 

Các cặp góc đối đỉnh trên hình vẽ là: aId và bIc ; aIc và bId

b) 

• Vẽ góc $\widehat{xOy}$

• Vẽ tia Ot là tia đối của tia Ox

• Vẽ tia Oz là tia đối của tia Oy

Ta được $\widehat{tOz}$ đối đỉnh với $\widehat{xOy}$

c) Cặp góc $\widehat{xDy}$ và $\widehat{zDt}$ trong Hình 8a và cặp góc $\widehat{xMz}$ và $\widehat{tMy}$ trong Hình 8b không phải là các cặp góc đối đỉnh vì mỗi cạnh của góc này không là cạnh đối của một cạnh của góc kia

Ở Hình 8a, Dt không là tia đối của Dx hay Dy; Dz không là tia đối của Dx hay Dy

Ở Hình 8b, My là tia đối của Mx nhưng Mt không là tia đối của Mz.

Vận dụng 2:

Các góc đối đỉnh trong hình là:

$\widehat{DOB}$ và $\widehat{COA}$; 

$\widehat{BOC}$ và $\widehat{AOD}$

3. TÍNH CHẤT CỦA HAI GÓC ĐỐI ĐỈNH

HĐKP3:

a) $\widehat{O_{1}}$ = 135$^{\circ}$ ; $\widehat{O_{3}}$ = 135$^{\circ}$  $\widehat{O_{1}}$= $\widehat{O_{3}}$

b) $\widehat{O_{2}}$= 45$^{\circ}$ ; $\widehat{O_{2}}$= 45$^{\circ}$ =>$\widehat{O_{2}}$= $\widehat{O_{4}}$

Kết luận:

Hai góc đối đỉnh thì bằng nhau. 

Thực hành 3:

a) Góc đối đỉnh của $\widehat{yOv}$. là $\widehat{zOu}$ vì tia Oz đối tia Oy, Ou đối tia Ov

b) Ta có: $\widehat{uOz}$ = $\widehat{yOv}$ ( 2 góc đối đỉnh)

mà $\widehat{yOv}$=110$^{\circ}$  $\widehat{uOz}$=110$^{\circ}$ .

Vận dụng 3.

Ta có: $\widehat{uOz}$ = $\widehat{yOv}$ ( 2 góc đối đỉnh), 

mà $\widehat{yOv}$=110$^{\circ}$   $\widehat{uOz}$ =110$^{\circ}$

Mà $\widehat{uOt}$+$\widehat{tOz}$ = $\widehat{uOz}$ ( do $\widehat{uOt}$ , $\widehat{tOz}$ là 2 góc kề nhau)

  x + 40$^{\circ}$ = 110$^{\circ}$   x = 110$^{\circ}$ - 40$^{\circ}$ = 70$^{\circ}$

Vậy x = 70$^{\circ}$

* Chú ý:

Hai đường thẳng vuông góc

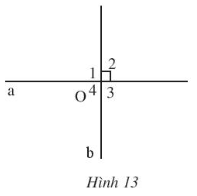
Hai đường thẳng a và b cắt nhau tại O tạo thành bốn góc $\widehat{O_{1}}$, $\widehat{O_{2}}$, $\widehat{O_{3}}$, $\widehat{O_{4}}$.

Do tính chất của hai góc đối đỉnh hoặc kề bù, ta nhận thấy trong số bốn góc nêu trên, nếu có một góc vuông thì ba góc còn lại cũng là góc vuông.

Khi đó ta nói hai đường thẳng a và b vuông góc với nhau và kí hiệu là a $\perp $ b hoặc b $\perp $ a.