I. SỐ HỮU TỈ

HĐ1:

Kết luận:

• Số hữu tỉ là số được viết dưới dạng phân số ab, với a, b ∈ Z; b ≠ 0.
• Tập hợp các số hữu tỉ được kí hiệu là Q.

Chú ý:

• Mỗi số nguyên là một số hữu tỉ.
• Các phân số bằng nhau là các cách viết khác nhau của cùng một số hữu tỉ.

Luyện tập 1: 

Ta có: 21 = $\frac{21}{1}$; -12 = $\frac{-12}{1}$; $\frac{-7}{-9}$= $\frac{7}{9}$

          -4,7 = $\frac{-47}{10}$; -3,05 = $\frac{-305}{100}$ = $\frac{-61}{20}$ 

=> Các số trên đều là số hữu tỉ.

II. BIỂU DIỄN SỐ HỮU TỈ TRÊN TRỤC SỐ

HĐ2: Biểu diễn số hữu tỉ $\frac{7}{10}$ trên trục số

Nhận xét: 

Do $\frac{14}{20}=\frac{7}{10}$ nên điểm A cũng là điểm biểu diễn số hữu tỉ $\frac{14}{20}$ trên trục số.

Kết luận:

• Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a
• Các phân số bằng nhau cùng biểu diễn một số hữu tỉ nên khi biểu diễn số hữu tỉ trên trục số, ta có thể chọn một trong những phân số đó để biểu diễn số hữu tỉ trên trục số. Thông thường ta chọn phân số tối giản để biểu diễn số hữu tỉ đó.

Luyện tập 2: Biểu diễn các số hữu tỉ: -0,3 trên trục số

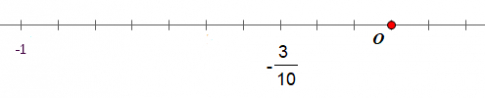
III. SỐ ĐỐI CỦA MỘT SỐ HỮU TỈ 

HĐ3: Điểm $\frac{5}{4}$ và $\frac{-5}{4}$ trên trục số cách đều và nằm về hai phía điểm gốc O.

Kết luận:

• Hai số hữu tỉ có điểm biểu diễn trên trục số và cách đều và nằm về hai phía điểm gốc O là hai số đối nhau, số này là số đối của số kia.
• Số đối của số hữu tỉ a kí hiệu là -a.
• Số đối của số 0 là 0 

Nhận xét:  Số đối của số -a là số a, tức là -(-a) = a

Luyện tập 3.

Số đối của các số $\frac{2}{9}$; -0,5 lần lượt là $\frac{-2}{9}$ và 0,5;

IV. SO SÁNH CÁC SỐ HỮU TỈ 

1. So sánh hai số hữu tỉ 

• Nếu số hữu tỉ a nhỏ hơn số hữu tỉ b thì ta viết a < b hay b > a
• Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương
• Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm 
• Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm 
• Nếu a < b và b < c thì a < c 

2. Cách so sánh hai số hữu tỉ 

HĐ4: (SGK – tr9)

Nhận xét:

• Khi hai số hữu tỉ cùng là phân số hoặc cùng là số thập phân, ta so sánh chúng theo những quy tắc đã biết ở lớp 6 
• Để so sánh hai số hữu tỉ, ta viết chúng về cùng dạng phân số hoặc cùng dạng số thập phân rồi so sánh chúng

Luyện tập 4.

a) Ta có: 3,23 < 3,32 nên -3,23 > -3,32

b) Ta có: $-\frac{7}{3}$ = $\frac{-28}{12}$; -1,25 = $\frac{-125}{100}$= $\frac{-5}{4}$ = $\frac{-15}{12}$

Vì -28 < -15 nên $\frac{-28}{12}$ < $\frac{-15}{12}$ hay $-\frac{7}{3}$ < -1,25

3. Minh họa trên trục số 

HĐ5: Với a < b, vị trí điểm a nằm bên trái so với điểm b trên trục số đó.

Kết luận:

• Khi so sánh hai số hữu tỉ, ta viết chúng ở dạng phân số có cùng mẫu số dương rồi so sánh hai tử số, tức so sánh hai số nguyên. Vì vậy, cũng như số nguyên, nếu x < y hay y > x thì điểm x nằm bên trái điểm y.
• Tương tự, nếu x < y hay y > x thì điểm x nằm phía dưới điểm y trên trục số thẳng đứng.