BÀI 23. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

1. Đường thẳng vuông góc với mặt phẳng

Bài 1: Đối với cánh cửa như trong Hình 7.10, khi đóng – mở cánh cửa, ta coi mép dưới BC của cánh cửa luôn sát sàn nhà (khe hở không đáng kể).

Đáp án: 

a) Đường thẳng AB cố định vì luôn đi qua hai bản lề cố định. Đường thẳng BC trên mặt sàn và luôn đi qua điểm B cố định (là giao của đường thẳng AB và mặt sàn). 

Vì đường thẳng BC quay quanh điểm B và (AB,BC)=90$^{\circ}$ nên AB vuông góc với các đường thẳng trên mặt sàn và đi qua B.

b) Theo tính chất của góc phẳng, khi hai đường thẳng AB và BC vuông góc với một đường thẳng CD chung, thì AB cũng vuông góc với BC. Vì vậy, khi đường thẳng AB vuông góc với đường thẳng đi qua điểm B trên sàn nhà, thì đường thẳng AB cũng vuông góc với mọi đường thẳng khác trên sàn nhà.

Bài 2: Nếu đường thẳng Δ và mặt phẳng (P) vuông góc với nhau thì chúng có cắt nhau hay không? 

Đáp án: 

Nếu ∆ $\perp $ (P) thì chúng có cắt nhau.

Bài 3: Gấp tấm bìa cứng hình chữ nhật…

Đáp án: 

a) Ta được 2 hình chữ nhật ABCD, ABMN => AB⊥AD, AB⊥AN.

b) Đặt ê ke như mô tả trong hình vẽ. Ta thấy một cạnh của ê ke trùng với AB và một cạnh thuộc a nên AB ⊥  a.

Bài 4: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì đường thẳng đó có vuông góc với các cạnh còn lại hay không? 

Đáp án: 

Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì đường thẳng đó có vuông góc với các cạnh còn lại.

Bài 5: Cho hình chóp S.ABCD…

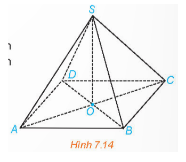
Đáp án: 

Ta có: SA = SC, SB = SD và O = AC ∩ BD nên O là trung điểm của AC, BD.

=> SO là trung tuyến của △SAC và △SBD

=> SO⊥AC, SO⊥BD ⇒SO⊥ABCD.

Bài 6: Khi làm cột treo quần áo, ta có thể tạo hai thanh đế thẳng đặt dưới sàn nhà và dựng cột treo vuông góc với hai thanh đế đó (H.7.15). Hãy giải thích vì sao bằng cách đó ta có được cột treo vuông góc với sàn nhà. 

Đáp án: 

Vì cột treo vuông góc với hai thanh đế, hai thanh đế đó cắt nhau và nằm trên mặt phẳng là sàn nhà nên cột vuông góc với sàn nhà (chứa hai thanh đế).

2. Tính chất

Bài 1: Cho điểm O và đường thẳng Δ…

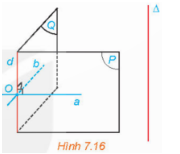
Đáp án: 

Ta có: 

$\left\{\begin{matrix}a\perp d & \\ d//\Delta  & \end{matrix}\right.$.⇒Δ⊥a

$\left\{\begin{matrix}b\perp d & \\ d//\Delta  & \end{matrix}\right.$⇒Δ⊥b

Mà a$\cap $b={O}⇒mp(a,b) đi qua O và vuông góc với Δ.

Bài 2: Cho mặt phẳng (P) và điểm O…

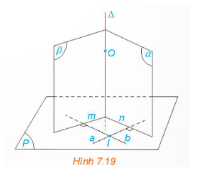
Đáp án: 

a) ($\alpha $),($\beta $) có điểm chung O và giao 2 mặt phẳng là 1 đường đường thẳng nên  ($\alpha $),($\beta $) cắt nhau theo một đường thẳng đi qua O.

b) Ta có: đi qua O

a⊥($\alpha $) Δ⊂($\beta $) =>a⊥Δ

b⊥($\beta $) Δ⊂($\beta $) => b⊥Δ

Mà a$\cap $b={I}⇒Δ⊥(P)

Bài 3: Cho ba điểm phân biệt A, B, C sao cho các đường thẳng AB và AC cùng vuông góc với một mặt phẳng (P). Chứng minh rằng ba điểm A, B, C thẳng hàng. 

Đáp án: 

Ta có: AB⊥(P);AC⊥(P)

Mặt khác, qua điểm A có duy nhất đường thẳng vuông góc với (P).

⇒A, B, C thẳng hàng.

3. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng

Bài 1: Cho đường thẳng a vuông góc với mặt phẳng (P) và song song với đường thẳng b. Lấy một đường thẳng m bất kì thuộc mặt phẳng (P). Tính (b, m) và từ đó rút ra mối quan hệ giữa b và (P).

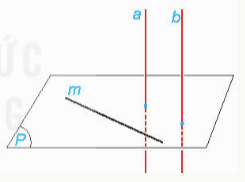
Đáp án: 

Vì a$\perp $(P) => a$\perp $m => (a,m)=90$^{\circ}$.

Mặt khác b // a => (b,m)=(a,m)=90$^{\circ}$.

Mà m $\in $ (P)⇒b⊥(P).

Bài 2: Cho hai đường thẳng phân biệt a và b cùng vuông góc với mặt phẳng (P). Xét O là một điểm thuộc a nhưng không thuộc b. Gọi c là đường thẳng qua O và song song với b.

a) Hỏi c có vuông góc với (P) hay không? Nhận xét về vị trí tương đối giữa a và c.

b) Nêu nhận xét về vị trí tương đối giữa hai đường thẳng a và b.

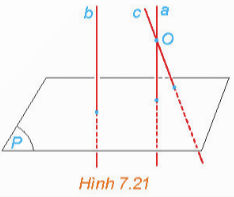
Đáp án: 

a) Ta có: b // c; b⊥(P) c ⊥(P)

Mà a ⊥(P); a, c cùng đi qua điểm O

=> a trùng c.

b) b //c mà a ≡ c => a//b.

Bài 3: Cho hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng  vuông góc với (P). Gọi b là một đường thẳng bất kì thuộc (Q). Lấy một đường thẳng a thuộc (P) sao cho a song song với b (H.7.23). So sánh ($\Delta $, b) và ($\Delta $, a). Từ đó rút ra mối quan hệ giữa Δ và (Q).

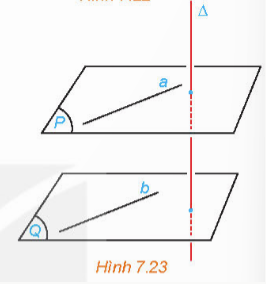
Đáp án: 

Ta có: ∆ $\perp $(P);a // b

(Δ,a)=(∆,b)=90$^{\circ}$

Do ∆ vuông góc mọi đường thẳng b trong (Q) => ∆ ⊥(Q).

Bài 4: Cho hai mặt phẳng phân biệt (P) và (Q) cùng vuông góc với đường thẳng Δ . Xét O là một điểm thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q). Gọi (R) là mặt phẳng đi qua O và song song với (Q) (H.7.24).

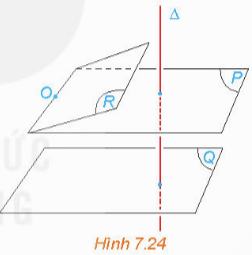
a) Hỏi (R) có vuông góc với Δ hay không? Nêu nhận xét về vị trí tương đối giữa (P) và (R).

b) Nêu vị trí tương đối giữa (P) và (Q).

Đáp án: 

a) (R) // (Q); Δ⊥ (Q) ⇒Δ⊥ (R)

Mà Δ⊥(P) và (R),(Q) cùng đi qua O ⇒(R) trùng (P)

b) (R)//(Q) mà (R) ≡ (P) => (P)//(Q).

Bài 5: Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn. Hỏi hai mặt phẳng đó có song song với nhau hay không? Vì sao? 

Đáp án: 

Hai mặt phẳng đó song song vì hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng (đường chứa một trong các chân bàn) thì song song với nhau.

Bài 6: Cho đường thẳng a song song với mặt phẳng (P) và đường thẳng Δ vuông góc với mặt phẳng (P). Tính (Δ, a).

Đáp án: 

Vì a //(P) nên a //b trong (P) => (∆,a)=(∆,b)

Mặt khác ∆ $\perp $ (P) nên (∆,a)=(∆,b)=90$^{\circ}$.

Bài 7: Cho đường thẳng a và mặt phẳng (P) cùng vuông góc với một đường thẳng Δ.

a) Qua một điểm O thuộc (P), kẻ đường thẳng a song song với a. Nêu vị trí tương đối giữa a' và (P).

b) Nêu vị trí tương đối giữa a và (P).

Đáp án: 

a) Ta có: a // a’ và  ∆ ⊥a => ∆ ⊥a'.

a’ đi qua O mà O ∈(P) và a'⊥∆

=> a'$\subset $(P)

b) Vì a // a’;  a'$\subset $(P)

=> a⊂(P) hoặc a // (P) 

Bài 8: Cho hình chóp S.ABCD…

Đáp án: 

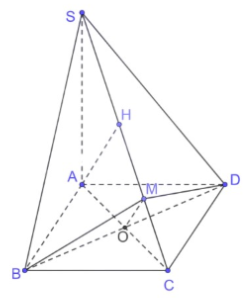
Ta có:

+) AC⊥BD (ABCD là hình vuông)

SA$\perp $BD(SA$\perp $ABCD) 

AC$\cap $SA={A} 

BD⊥(SAC)

+) BD$\perp $SC(BD⊥(SAC))

BM⊥SC

BD⊥BM={B}

⇒SC⊥(MBD)

Gọi AC∩BD={O}

Lại có: SC⊥MBD;OM⊂(MBD) (cmt)

⇒SC⊥OM. Mà AH$\perp $SC

AH//OM,OM⊂(MBD)⇒AH // (MBD).

4. Bài tập

Bài 7.5: Cho hình chóp S.ABC có đáy là tam giác cân…

Đáp án: 

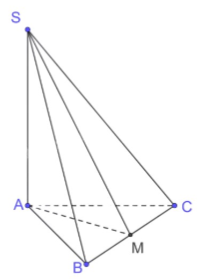
a) Xét △ABC cân tại A có: 

AM vừa là đường trung tuyến (M là trung điểm BC) vừa là đường cao

=> AM⊥BC 

Ta có: AM⊥BC (cmt) SA⊥BC (SA⊥(ABC)) AM$\cap $SA={A} => BC⊥(SAM)

b) Ta có: BC⊥(SAM) SM⊂(SAM) => BC⊥SM 

Xét △SBC có:

SM vừa là đường cao (BC⊥SM) vừa là đường trung tuyến (M là trung điểm BC)

=> △SBC cân tại S.

Bài 7.6: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ⊥ (ABCD). Chứng minh rằng các mặt bên của hình chóp S.ABCD là các tam giác vuông. 

Đáp án: 

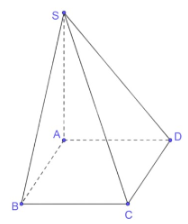
Ta có:

+) BC$\perp $AB (ABCD là hcn); SA$\perp $BC (SA⊥(ABCD)) AB$\cap $SA={A}

=> BC$\perp $(SAB); SB⊂(SAB) => BC$\perp $SB

+) CD$\perp $AD(ABCD là hcn) CD$\perp $SA (SA⊥(ABCD)) AD$\cap $SA={A} => CD⊥(SAD);SD⊂(SAD) => CD⊥SD

+) Xét △SAB có SA$\perp $AB (gt) △SAB vuông tại A. 

Xét △SBC có SB$\perp $BC (cmt) △SBC vuông tại B.

Xét △SCD có SD$\perp $CD (cmt) △SCD vuông tại D.

Xét △SAD có SA$\perp $AD(gt)  △SAD vuông tại A.

Bài 7.7: Cho hình chóp S.ABCD có đáy là hình chữ nhật…

Đáp án: 

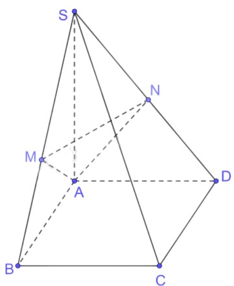
+) BC$\perp $AB (ABCD là hcn); BC$\perp $SA (SA⊥(ABCD); AB$\cap $SA={A}

BC⊥(SAB);AM⊂(SAB) => BC$\perp $AM

+) CD$\perp $AD (ABCD là hcn); CD$\perp $SA (SA⊥(ABCD); AD$\cap $SA={A}

CD⊥(SAD);AN⊂(SAD) CD⊥AN

+) AM$\perp $SB; AM$\perp $BC; SB$\cap $BC={B} =>AM⊥(SBC);SC⊂(SBC)

SC⊥AM

+) AN$\perp $SD; AN⊥CD; SD$\cap $CD={D} => AN⊥(SCD);SC⊂(SCD)

SC⊥AN

+) AM$\perp $SC; AN⊥SC; AM$\cap $AN={A} => SC$\perp $(AMN).

Bài 7.8: Bạn Vinh thả quả dọi chìm vào thùng nước. Hỏi khi dây dọi căng và mặt nước yên lặng thì đường thẳng chứa dây dọi có vuông góc với mặt phẳng chứa mặt nước trong thùng hay không? 

Đáp án: 

Khi dây dọi căng và mặt nước yên lặng, đường thẳng chứa dây dọi vuông góc với mặt phẳng nước chứa mặt nước trong thùng.

Bài 7.9: Một cột bóng rổ được dựng trên một sân phẳng…

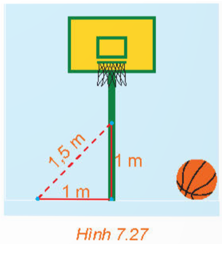
Đáp án: 

Nếu phép đo của Hùng là chính xác ta có 1$^{2}$+1$^{2} \neq $1,5$^{2}$ 

Do đó theo định lý Pythagore thì cột cờ không vuông góc với mặt sân.

Vậy cột không có phương thẳng đứng.