BÀI 24. PHÉP CHIẾU VUÔNG GÓC. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG

1. Phép chiếu vuông góc

Bài 1: Trên sân phẳng có một cây cột thẳng vuông góc với mặt sân…

Đáp án: 

a) Bóng của cột trên sân có thể được nhìn như hình chiếu của cây cột.

b) Ta không thể quan sát vì khi tia sáng mặt trời vuông góc với mặt sân thì hình chiếu của cột thu về chân cột

Bài 2:

a) Nếu A là một điểm không thuộc mặt phẳng (P) và A’ là hình chiếu của A trên (P) thì đường thẳng AA’ có quan hệ gì với mặt phẳng (P)?

b) Nếu đường thẳng a vuông góc với mặt phẳng (P) thì hình chiếu của a trên (P) là gì? 

Đáp án: 

a) AA’$\perp $(P).

b) Hình chiếu vuông góc của đường thẳng a trên (P) là một điểm, là giao điểm của a và (P).

Bài 3: Cho đường thẳng a và mặt phẳng (P) không vuông góc với nhau…

Đáp án: 

a) Hình chiếu vuông góc của a trên (P) là M'N'.

b) b⊥M'N';b⊥MM'(MM'$\perp $(P))

⇒b⊥(a,a')⇒b⊥a. 

c) b⊥a;b⊥MM'(MM'$\perp $(P))

⇒b⊥(a,a')⇒b⊥M'N'. 

Bài 4: Cho hình chóp S.ABC có SA = SB = SC…

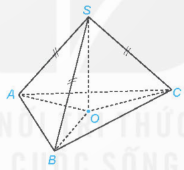
Đáp án: 

a) Do SO⊥(ABC) và SA=SB=SC nên △SOA= △SOB= △SOC

=> OA=OB=OC.  

Vậy O là tâm đường tròn ngoại tiếp △ABC.

b) O là hình chiếu của S trên (ABC)

A là hình chiếu của A trên (ABC) 

=> Hình chiếu của SA trên (ABC) là OA.

c) Ta có SO⊥(ABC) nên SO⊥BC; AO⊥BC; AO ∩ SO = {O} 

=> BC⊥ (SOA )=> BC⊥SA.

d) Ta có:

O là hình chiếu của S trên (ABC)

A là hình chiếu của A trên (ABC)

B là hình chiếu của B trên (ABC)

C là hình chiếu của C trên (ABC)

=> Hình chiếu của mỗi tam giác SBC,SCA, SAB trên mặt phẳng (ABC) lần lượt là △OBC,OCA,OAB.

2. Góc giữa đường thẳng và mặt phẳng

Bài 1: Một máy bay giữ vận tốc không đổi, với độ lớn 240km/h trong suốt 2 phút đầu kể từ khi cất cánh. Hỏi thông tin trên có đủ để ta xác định độ cao của máy bay so với mặt đất phẳng, tại thời điểm 1 phút kể từ khi máy bay cất cánh không?

Đáp án: 

Thông tin chưa đủ để xác định độ cao mà chỉ tính được quãng đường bay bay được.

 Bài 2: Tâm Trái Đất chuyển động quanh Mặt Trời theo quỹ đạo là một đường elip…

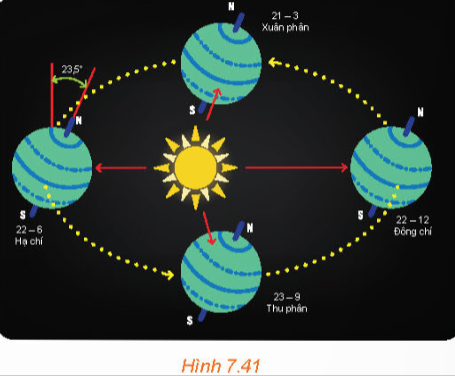
Đáp án: 

a) Gọi a là một vị trí của trục Trái Đất; a'tương ứng là hình chiếu của a trên (P).

Nếu a có phương không đổi thì hình chiếu của a lên (P) có phương không đổi; nên a'có phương không đổi.

Gọi b là một vị trí trục của Trái Đất khác trục a; b'tương ứng là hình chiếu của b trên (P).

Ta có: a, b có phương khác phương chiếu; a//b.

⇒a'//b’ hoặc a'và b' trùng nhau (tính chất phép chiếu song song).

Vậy hình chiếu của trục Trái Đất có phương không đổi.

b) Gọi m là đường thẳng đi qua tâm Mặt Trời và có phương là phương chiếu của trục Trái Đất trên (P).

Suy ra m có phương không đổi.

Khi đó hình chiếu của trục Trái Đất xuống (P) thuộc đường thẳng m khi và chỉ khi tâm Trái Đất là giao của m với đường elip quỹ đạo của Trái Đất.

Vậy có hai vị trí thuộc quỹ đạo, ứng với hai thời điểm trong năm mà hình chiếu của trục Trái Đất trên (P) thuộc đường thẳng nối tâm Mặt Trời và tâm Trái Đất.

Bài 3: Cho đường thẳng Δ vuông góc với mặt phẳng (P). Khi đó, với một đường thẳng a bất kì, góc giữa a và (P) có mối quan hệ gì với góc giữa a và Δ? 

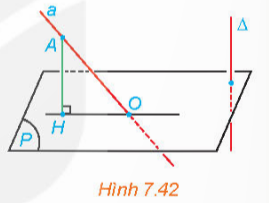
Đáp án: 

Trường hợp 1. Đường thẳng a không vuông góc với (P) và cắt (P) tại một điểm O. Lấy điểm A khác O thuộc a và gọi H là hình chiếu vuông góc của A trên (P).

Δ//a và (Δ,a)=(AH,a)=$\widehat{HAO}$=90$^{\circ}$-(a,P).

Vậy (a, ) phụ với (a, (P)) 

Trường hợp 2: a $\perp $ (P). 

a//Δ và (a,Δ)=0$^{\circ}$,(a,P)=90$^{\circ}$.  

Trường hợp 3: a // hoặc ∈ (P).

a⊥Δ và (a,Δ)=90$^{\circ}$,(a,P)=0$^{\circ}$.

Như vậy kết luận đã nêu trong trường hợp 1 cũng đúng đối với cả hai trường hợp sau. 

3. Bài tập

Bài 7.10: Cho hình chóp S.ABC có SA ⊥ (ABC)…

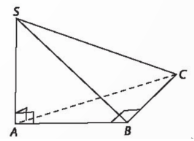
Đáp án: 

a) Ta có: SA $\perp $ (ABC) => A là hình chiếu của S trên (ABC)

b) A là hình chiếu của S trên (ABC)

B là hình chiếu của B trên(ABC)

C là hình chiếu của C trên (ABC)

⇒ Hình chiếu của △SBC trên (ABC) là △ABC.

c) B là hình chiếu của C trên (SAB)

S, B là hình chiếu của chính nó trên (SAB)

⇒ Hình chiếu của △SBC trên (SAB) là SB.

Bài 7.11: Cho hình chóp S.ABCD có đáy là hình vuông ABCD…

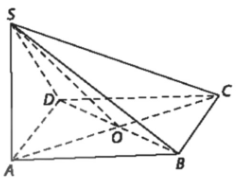
Đáp án: 

a) A là hình chiếu của S trên (ABCD) (SA⊥(ABCD))

C là hình chiếu của C trên (ABCD) 

=> AC là hình chiếu của SC trên (ABCD)

⇒(SC,(ABCD))=(SC,AC)=$\widehat{SCA}$

Xét △ABC vuông tại B có:

AC$^{2}$=AB$^{2}$+BC$^{2}$ (định lí Pythagore)

=2a$^{2}$ => AC=a$\sqrt{2}$ 

Xét △SAC vuông tại A có: tan⁡$\widehat{SCA}$=$\frac{SA}{AC}$=$\frac{A\sqrt{2}}{A\sqrt{2}}$=1⇒$\widehat{SCA}$=45$^{\circ}$

Vậy (SC,(ABCD))=45$^{\circ}$

b)  AC$\perp $BD (ABCD là hình vuông) SA$\perp $BD (SA⊥(ABCD)) AC$\cap $SA={A} 

=> BD$\perp $(SAC)⇒(BD,(SAC))=90$^{\circ}$

c) Gọi AC$\cap $BD={O} mà BD⊥(SAC)

=> O là hình chiếu của B trên (SAC)

Vậy hình chiếu của SB trên (SAC) là SO.

Bài 7.12: Cho hình chóp S.ABC có SA ⊥ (ABC)… 

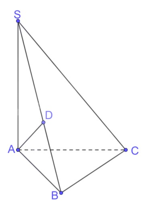
Đáp án: 

a) Trong (SAB) kẻ AD$\perp $SB tại D.

BC$\perp $AD SB$\perp $AD BC$\cap $SB={B} => AD⊥(SBC)⇒ D là hình chiếu của A trên (SBC).

b) A là hình chiếu của S trên (ABC) (SA⊥(ABC)); C là hình chiếu của C trên (ABC) 

=> AC là hình chiếu của SC trên (ABC)⇒(SC,(ABC))=(SC,AC)=$\widehat{SCA}$

Xét △ABC vuông tại B có:

AC$^{2}$=AB$^{2}$+BC$^{2}$ (định lí Pythagore)

=2a$\sqrt{2}$ => AC=a$\sqrt{2}$

Xét △SAC vuông tại A có: tan⁡$\widehat{SCA}$=$\frac{SA}{AC}$=$\frac{a}{a\sqrt{2}}$=$\frac{1}{\sqrt{2}}$ => $\widehat{SCA}$=arctan⁡$\frac{1}{\sqrt{2}}$ 

=> (SC,(ABCD))=arctan$\frac{1}{\sqrt{2}}$

Bài 7.13: Cho điểm S nằm ngoài mặt phẳng (P)…

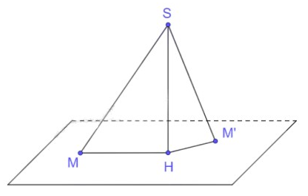
Đáp án: 

a) +) Giả sử SM=SM'

∆SHM=∆SHM' (cạnh huyền – cạnh góc vuông) ⇒HM=HM' (cạnh tương ứng)

+) Giả sử HM=HM'

∆SHM=∆SHM' (hai cạnh góc vuông) ⇒SM=SM' (cạnh tương ứng)

Vậy SM=SM' ⬄ HM=HM'.

b) Ta có: MH>M’H 

⇔MH$^{2}$>M'H$^{2}$

⇔MH$^{2}$+SH$^{2}$>M'H$^{2}$+SH$^{2}$

<=> SM$^{2}$>SM'$^{2}$ <=> SM>SM'

Bài 7.14: Trong một khoảng thời gian đầu kể từ khi cất cánh…

Đáp án: 

2 máy bay cùng bay được quãng đường dài s=1.v=v(m) sau 1 phút

Máy bay 1 đã bay tới độ cao là: 

h$_{1}$=s.sin sin 10$^{\circ}$ =v.sin10$^{\circ}$≈0,17v

Máy bay 2 đã bay tới độ cao là: 

h$_{2}$=s.sin sin 15$^{\circ}$ =v.sin15$^{\circ}$≈0,26v

=> Sau 1 phút từ khi cất cánh, máy bay 2 có độ cao cao hơn máy bay 1.

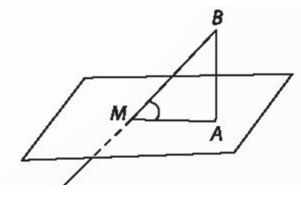
Bài 7.15: Hãy nêu cách đo góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang tại một vị trí và một thời điểm. 

Đáp án: 

Giả sử có một cột AB, bóng của cột AB là AM.

Ta tính được: tan tan $\widehat{BMA}$=$\frac{AB}{AM}$ . Từ đó tính được $\widehat{BMA}$ cần tìm