Bài 1 trang 52 SBT Toán 8 tập 1 CTST: Cho tam giác MNP vuông tại M.

a) Tính độ dài cạnh NP nếu biết MN = 7, MP = 24.

b) Tính độ dài cạnh MP nếu biết NP = 29, MN = 20.

c) Tính độ dài cạnh MN nếu biết NP = 61, MP = 11.

Giải

a) Áp dụng định lý Pythagore vào tam giác MNP vuông tại M, ta có:

$NP^{2} = MN^{2} + MP^{2} = 7^{2} + 24^{2} = 49 + 576 = 625$

$ \Rightarrow  NP = \sqrt {625} = 25$

b) Từ $NP^{2} = MN^{2} + MP^{2}$

$\Rightarrow MP^{2} = NP^{2} ‒ MN^{2} = 29^{2} ‒ 20^{2} = 441$

$\Rightarrow MP = \sqrt{441} = 21$

c) Từ $NP^{2} = MN^{2} + MP^{2}$, 

$\Rightarrow MN^{2} = NP^{2} ‒ MP^{2} = 61^{2} ‒ 11^{2} = 3600$

$\Rightarrow MN = \sqrt {3600} =60$

Bài 2 trang 52 SBT Toán 8 tập 1 CTST: Chứng minh tam giác EFG vuông trong các trường hợp sau:

a) FG = 12, EF = 35, EG = 37;

b) FG = 85, EF = 77, EG = 36;

c) FG = 12, EF = 13, EG = 5.

Giải 

a) Ta có $EG^{2} = 37^{2} = 1 369$ và $EF^{2} + FG^{2} = 35^{2} + 12^{2} = 1 369$.

Suy ra tam giác EFG vuông tại F (định lí Pythagore đảo).

b) Ta có $FG^{2} = 85^{2} = 7 225$ và $EF^{2} + EG^{2} = 77^{2} + 36^{2} =7 225$.

Suy ra tam giác EFG vuông tại E (định lí Pythagore đảo).

c) Ta có $EF^{2} = 13^{2} = 169$ và $EG{2} + FG^{2} = 12^{2} + 5^{2} = 169$.

Suy ra tam giác EFG vuông tại G (định lí Pythagore đảo).

Bài 3 trang 52 SBT Toán 8 tập 1 CTST: Tính chiều cao BH của tam giác ABC cân tại B (Hình 5), biết AB = 9 cm và AC = 4 cm.

Giải

Tam giác ABC cân tại B nên đường cao BH cũng là đường trung tuyến.

$\Rightarrow AH =\frac{AC}{2} = \frac{4}{2} = 2 cm$

Áp dụng định lí Pythagore vào tam giác ABH vuông tại H, ta có:

$AB^{2} = AH^{2} + BH^{2}$

Suy ra $BH^{2} = AB^{2} – AH^{2} = 9^{2} – 2^{2} = 77$

Do đó $BH= \sqrt{77} cm $.

Bài 4 trang 52 SBT Toán 8 tập 1 CTST: Tính độ dài x trong Hình 6.

Giải

Áp dụng định lí Pythagore vào tam giác BCD vuông tại C, ta có:

$BD^{2} = BC^{2} + CD^{2}$

Suy ra: $BC^{2} = BD^{2} ‒ CD^{2} = 19^{2} ‒ 13^{2} = 192$.

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:

$BC^{2} = AB^{2} + AC^{2}$

Suy ra: $AB^{2} = BC^{2} ‒ AC^{2} = 192 ‒ 5^{2} = 167$

Do đó $AB = x - \sqrt{167}$.

Bài 5 trang 52 SBT Toán 8 tập 1 CTST: Tính độ dài các cạnh chưa biết của tam giác vuông sau:

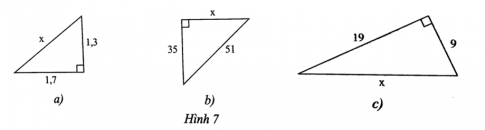
Giải

Áp dụng định lý Pythagore trong tam giác vuông ta có:

a) $x^{2} = 1,3^{2} + 1,7^{2} = 4,58$

$ \Rightarrow x = \sqrt{4,58} \approx 2,1$

b) $51^{2} = 35^{2} + x^{2}$

Suy ra $x^{2} = 51^{2} – 35^{2} = 1376$.

Do đó $x = \sqrt{1376} \approx  37$

c) $x^{2} = 19^{2} + 9^{2} = 44^{2}$.

Suy ra $x = \sqrt{442} \approx 21$

Bài 6 trang 52 SBT Toán 8 tập 1 CTST: Tìm tam giác vuông trong các tam giác sau:

Giải

a) Vì $41^{2} = 1681 ≠ 1664 = 40^{2} + 8^{2}$ nên Hình 8a không là tam giác vuông.

b) Vì $65^{2} = 4225 = 52^{2} + 39^{2}$ nên theo định lí Pythagore thì Hình 8b là tam giác vuông.

c) Vì $65^{2} = 4225 ≠ 4148 = 58^{2} + 28^{2}$ nên Hình 8c không là tam giác vuông.

Bài 7 trang 53 SBT Toán 8 tập 1 CTST: Tính khoảng cách x từ đầu thang đến chân tường (Hình 9).

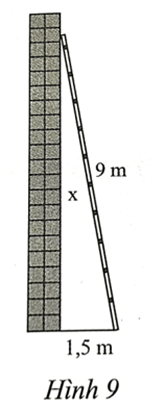
Giải

Khoảng cách x từ đầu thang đến chân tường bằng độ dài cạnh góc vuông trong tam giác vuông nên áp dụng định lý Pythagore trong tam giác vuông ta có:

$9^{2} = x^{2} + 5^{2}$, suy ra $x = \sqrt{9^{2} - 1,5^{2}} \approx 8,9 (m)$

Bài 8 trang 53 SBT Toán 8 tập 1 CTST: Một máy bay đang ở độ cao 5,2 km. Khoảng cách từ hình chiếu vuông góc của máy bay xuống mặt đất đến vị trí A của sân bay là 10,2 km (Hình 10). Tính khoảng cách từ vị trí máy bay đến vị trí A của sân bay.

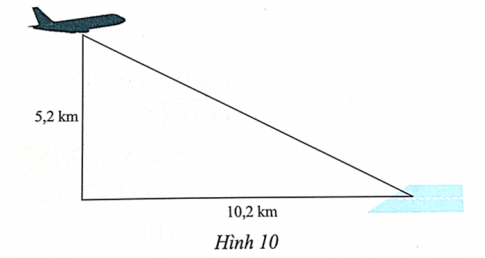
Giải

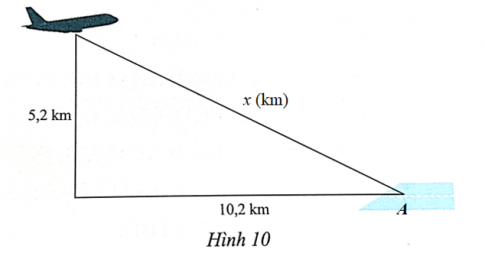
Gọi khoảng cách từ vị trí máy bay đến vị trí A của sân bay là x(km) (x > 0).

Khoảng cách từ vị trí máy bay đến vị trí A của sân bay là độ dài cạnh huyền trong tam giác vuông nên áp dụng định lý Pythagore trong tam giác vuông ta có:

$x^{2} = \sqrt{5,2^{2} + 10,2^{2}} \approx 11,4$

Vậy khoảng cách từ vị trí máy bay đến vị trí A của sân bay là khoảng 11,4 km.