CHƯƠNG 3. ĐỊNH LÝ PYTHAGORE. CÁC LOẠI TỨ GIÁC THƯỜNG GẶP

BÀI 1. ĐỊNH LÝ PYTHAGORE

1. ĐỊNH LÝ PYTHAGORE

HĐKP1:

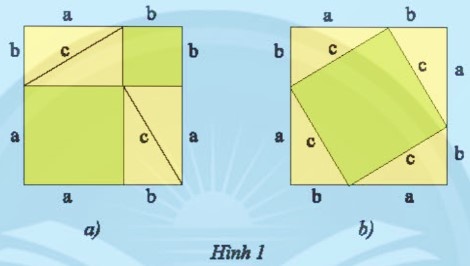
+ Diện tích hình vuông có cạnh bằng a là: $a^{2}$ (đơn vị diện tích).

Diện tích hình vuông có cạnh bằng b là: $b^{2}$ (đơn vị diện tích).

+ Diện tích phần bìa không bị che lấp trong hình vuông lớn ở Hình 1a là:

$a^{2}+b^{2}$ (đơn vị diện tích).

+ Diện tích phần bìa không bị che lấp trong hình vuông lớn ở Hình 1b chính là diện tích hình vuông có cạnh bằng c, và bằng: $c^{2}$ (đơn vị diện tích).

+ Trong cả hai hình đều đặt bốn tam giác vuông lên hai hình vuông lớn có cạnh bằng a + b.

+ Khi đó diện tích phần bìa không bị che lấp của cả hai hình sẽ bằng nhau.

Do đó $a^{2}+b^{2}=c^{2}$

=> Kết luận:

Định lí Pythagore:

Trong một tam giác vuông, bình phương độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.

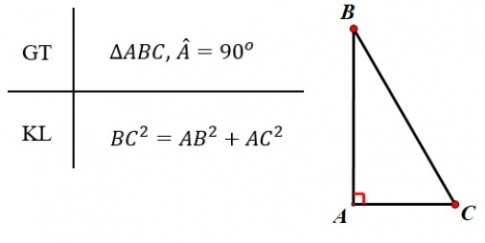
Ví dụ 1: (SGK – tr59)

Thực hành 1:

a)

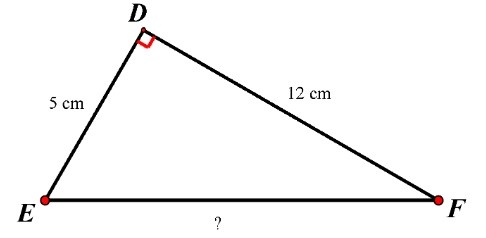
Xét tam giác vuông DEF có:

$EF^{2} = DE^{2} + DF^{2}$ (ĐL Pythagore)

$EF^{2} = 5^{2} + 12^{2} = 25 + 144 = 169$

EF=13 (cm)

b) 

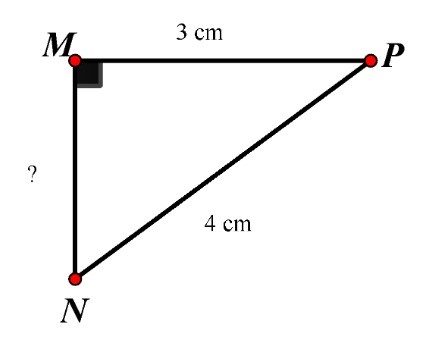
Xét tam giác vuông DEF có:

$NP^{2} = MN^{2} + MP^{2}$ (ĐL Pythagore)

$MN^{2} = NP^{2} - MP^{2} = 4^{2}-3^{2}= 7$

$MN=\sqrt{7}$ (cm)

Vận dụng 1:

Chiếc ti vi ở Hình 4 được mô tả bởi tam giác ABC vuông tại A có các kích thước như hình vẽ sau:

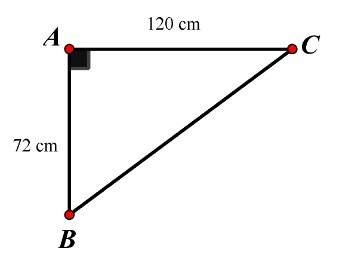
Xét tam giác vuông ABC có:

$BC^{2} = AB^{2} + AC^{2}$ (ĐL Pythagore)

$BC^{2} = 72^{2}+120^{2} = 5 184+14 400= 19 584$

$BC=24\sqrt{34}$ ≈139,94 (cm) ≈55,09 (inch)

2. ĐỊNH LÝ PYTHAGORE ĐẢO 

HĐKP2.

Ta vẽ tam giác ABC có AB = 12 cm, AC = 5 cm, BC = 13 cm như sau:

+ Vẽ đoạn thẳng AB = 12 cm;

+ Vẽ cung tròn tâm A bán kính 5 cm và cung tròn tâm B bán kính 13 cm. Hai cung tròn này cắt nhau tại một điểm, điểm này là điểm C.

Dùng thước đo góc (đặt thước như hình vẽ trên) ta xác định được BAC = $90^{o}$

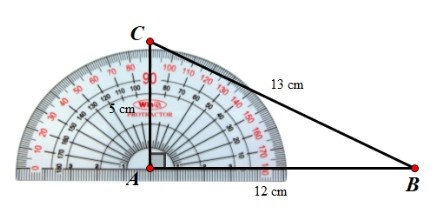
=> Kết luận:

Định lý Pythagore đảo:

Nếu một tam giác có bình phương độ dài của một cạnh bằng tổng các bình phương độ dài của hai cạnh kia thì tam giác đó là tam giác vuông.

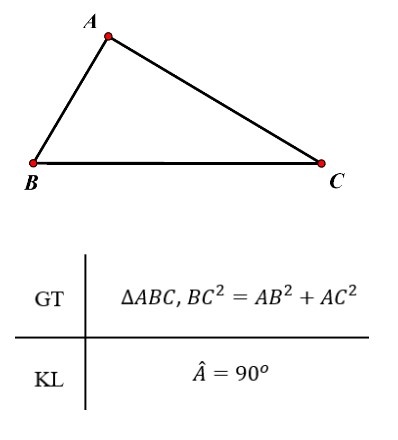
Ví dụ 2: SGK – tr60

Thực hành 2. 

a) Ta có: 

$EK^{2}=15^{2} =225$

$EF^{2}+EK^{2}= 9^{2} + 12^{2}=225$

Suy ra $EK^{2} = EF^{2} + FK^{2}$

Vậy tam giác EFK vuông tại F.

b) Ta có PQ là cạnh dài nhất 

mà $PQ^{2}=17^{2} =289$

$PR^{2}+QR^{2}= 10^{2} + 12^{2}=244$

suy ra $PQ^{2}$ ≠ $PR^{2} + QR^{2}$.

Vậy tam giác PQR không phải là tam giác vuông.

c) Ta có: 

$EF^{2} =10^{2}=100$

$DF^{2} + DE^{2}= 6^{2} + 8^{2}=100$

Suy ra $EF^{2} =DF^{2} + DE^{2}$

Vậy tam giác DEF vuông tại D.

Vận dụng 2:

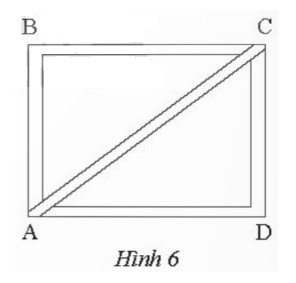
a) Giả sử chiếc êke mà Nam dự định làm được mô tả bởi tam giác ABC vuông tại A có kích thước như hình vẽ dưới đây: 

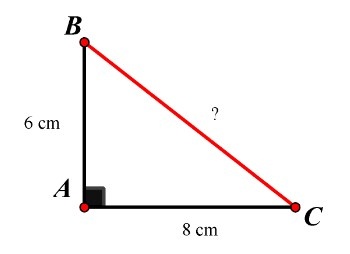
Xét tam giác ABC có BC là cạnh huyền, ta có:

$BC^{2} = AB^{2} + AC^{2}$  (ĐL Pythagore)

$= 6^{2} + 8^{2} = 36 + 64 = 100$

Suy ra BC = 10 cm.

Vậy thanh nẹp còn lại Nam phải làm có độ dài 10 cm.

b) Xét tam giác ABC có: 

$AB^{2} + BC^{2} = 36^{2} + 48^{2} = 3600$

$AC^{2} = 60^{2} = 3600$.

Do đó $AB^{2} + BC^{2} = AC^{2}$

Vậy tam giác ABC vuông tại B nên ABC là góc vuông.

Xét tam giác ADC có: 

$AD^{2} + DC^{2} = 48^{2} + 36^{2} = 3600$

$AC^{2} = 60^{2} = 3600$

Do đó $AD^{2} + DC^{2} = AC^{2}$.

Vậy tam giác ADC vuông tại D nên ADC là góc vuông.

3. VẬN DỤNG ĐỊNH LÍ PYTHAGORE

Thực hành 3: 

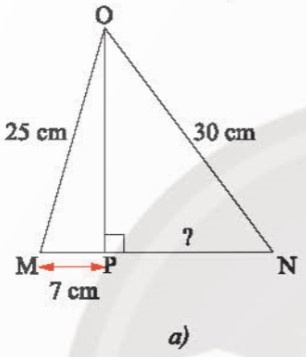
a) Áp dụng định lí Pythagore vào tam giác OPM vuông tại P, ta có:

$OM^{2} = OP^{2} + MP^{2}$

$OP^{2} = OM^{2}-MP^{2}$

$= 25^{2}-7^{2} = 576$.

Áp dụng định lí Pythagore vào tam giác OPN vuông tại P, ta có:

$ON^{2} = OP^{2} + PN^{2}$

⇒ $PN^{2} = ON^{2}-OP^{2}$

$= 30^{2}-576 = 324$

Vậy PN = 18 cm.

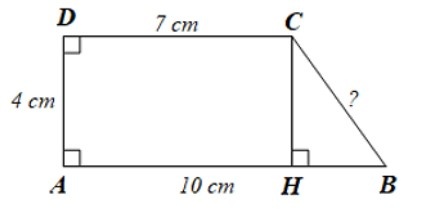
Vẽ CH vuông góc với AB như hình vẽ, ta có:

CH = 4 cm; HB = 10 – 7 = 3 cm.

Áp dụng định lí Pythagore vào tam giác CHB vuông tại H, ta có:

$BC^{2}=CH^{2} + HB^{2}$ 

$=4^{2} + 3^{2} =25$

Vậy BC = 5 cm.

Vận dụng 3:

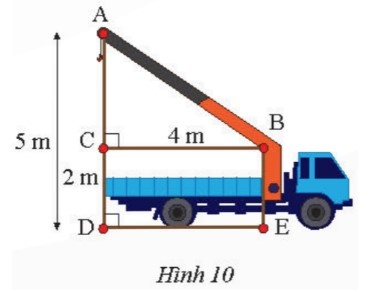
Xét tam giác ABC có:

 CB = 4 m, 

AC = AD – CD 

= 5 – 2 

= 3 (m).

Áp dụng định lí Pythagore cho tam giác ABC vuông tại C, ta có:

$AB^{2} =AC^{2} + CB^{2} =3^{2} + 4^{2} =25$

Suy ra AB = 5 m.

Vậy chiều dài cần cẩu AB là 5 m.