Giải SBT Toán 8 Chân trời bài Bài tập cuối chương 2
Giải chi tiết sách bài tập Toán 8 tập 1 Chân trời sáng tạo bài Bài tập cuối chương 2. Tech12h sẽ hướng dẫn giải tất cả câu hỏi và bài tập với cách giải nhanh và dễ hiểu nhất. Hi vọng, thông qua đó học sinh được củng cố kiến thức và nắm bài học tốt hơn.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
A. CÂU HỎI TRẮC NGHIỆM
Câu 1 trang 44 SBT Toán 8 tập 1 CTST: Hình nào sau đây là hình chóp tam giác đều?
A. Hình có đáy là tam giác.
B. Hình có đáy là tam giác đều.
C. Hình có đáy là tam giác đều và tất cả các cạnh đều vuông góc với mặt đáy.
D. Hình có đáy là tam giác đều và tất cả các cạnh bên bằng nhau.
Giải
Đáp án đúng D. Hình có đáy là tam giác đều và tất cả các cạnh bên bằng nhau.
Câu 2 trang 44 SBT Toán 8 tập 1 CTST: Hình nào sau đây là hình chóp tứ giác đều?
A. Hình có đáy là tứ giác.
B. Hình có đáy là hình vuông.
C. Hình có đáy là hình vuông và tất cả các cạnh bên bằng nhau.
D. Hình có đáy là tam giác đều và có một cặp cạnh bên vuông góc với nhau.
Giải
Đáp án đúng C. Hình có đáy là hình vuông và tất cả các cạnh bên bằng nhau.
Hình chóp tứ giác đều có đáy là một tứ giác đều và tất cả các cạnh bên bằng nhau
Câu 3 trang 44 SBT Toán 8 tập 1 CTST: Cho hình chóp tam giác đều có cạnh đáy bằng 8 cm và chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tam giác đều bằng 10 cm. Diện tích xung quanh của hình chóp này là
A. 80 $cm^{2}$.
B. 120 $cm^{2}$.
C.240 $cm^{2}$.
D. 320 $cm^{2}$.
Giải
Đáp án đúng B. 120 $cm^{2}$
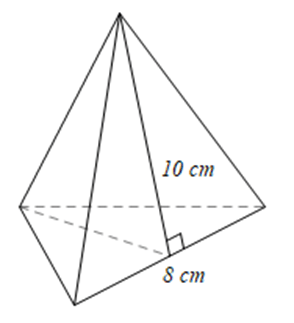
Diện tích xung quanh của hình chóp tam giác đều là:
$S_{xq} = 3.\frac{1}{2} 10 .8 = 120 (cm^{2})$
Câu 4 trang 44 SBT Toán 8 tập 1 CTST: Cho hình chóp tam giác đều có diện tích đáy bằng 36 cm và chiều cao bằng 9 cm. Thể tích của hình chóp này là
A. 54 $cm^{3}$.
B. 72 $cm^{3}$.
C. 108 $cm^{3}$.
D. 216 $cm^{3}$.
Giải
Đáp án đúng C. 108 $cm^{3}$.
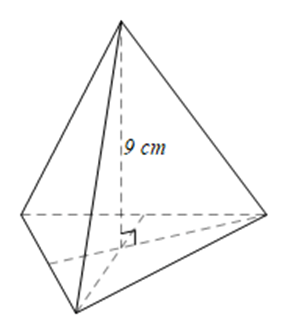
Thể tích hình chóp tam giác đều là: $V = \frac{1}{3} .36.9 = 108 (cm^{3})$
Câu 5 trang 45 SBT Toán 8 tập 1 CTST: Cho hình chóp tứ giác đều có cạnh đáy bằng 10 m và chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều bằng 12 m. Diện tích toàn phần của hình chóp này là
A. 200 $m^{2}$.
B. 340 $cm^{2}$.
C. 400 $cm^{2}$.
D. 340 $cm^{2}$.
Giải
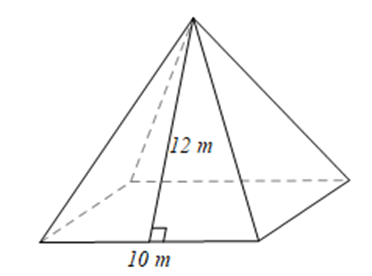
Diện tích toàn phần của hình chóp tứ giác đều là:
$S_{tp} = S_{đáy} + S_{xq} = 10^{2} + 4 . \frac{10.12}{2} = 340 (m^{2})$
Câu 6 trang 45 SBT Toán 8 tập 1 CTST: Cho hình chóp tứ giác đều có cạnh đáy bằng 5 m và chiều cao bằng 8 m. Thể tích của hình chóp này là
A. $\frac{200}{3} m^{3}$
B. $64 m^{3}$
C. $80 m^{3}$
D. $\frac{320}{3} m^{3}$
Giải
Đáp án đúng A. $\frac{200}{3} m^{3}$
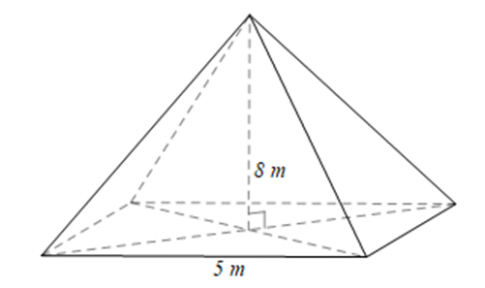
Thể tích của hình chóp tứ giác đều là:
$V = \frac{1}{3}. 5^{2} .8 = \frac{200}{3} (m^{3})$
B. BÀI TẬP TỰ LUÂN
Bài 7 trang 45 SBT Toán 8 tập 1 CTST: Hoàn thành bảng sau:
Hình chóp tam giác đều
| Hình chóp tứ giác đều
| |
Đỉnh | ? | ? |
Cạnh bên | ? | ? |
Cạnh đáy | ? | ? |
Mặt bên | ? | ? |
Mặt đáy | ? | ? |
Chiều cao | ? | ? |
Giải
Hình chóp tam giác đều
| Hình chóp tứ giác đều
| |
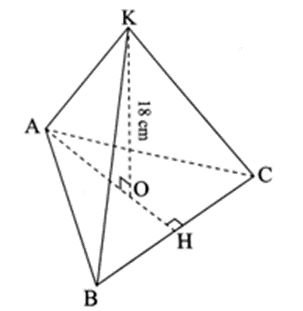
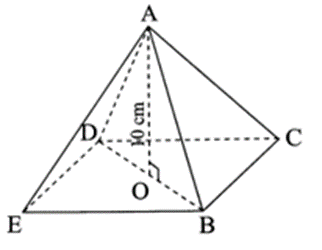
Đỉnh | K | A |
Cạnh bên | KA, KB, KC | AB, AC, AD, AE |
Cạnh đáy | AB, BC, CA | BC, CD, DE, EB |
Mặt bên | KAB, KBC, KCA | ABC, ACD, ADE, AEB |
Mặt đáy | ABC | BCDE |
Chiều cao | KO = 18 cm | AO =10 cm |
Bài 8 trang 46 SBT Toán 8 tập 1 CTST: Trong các miếng bìa sau, miếng bìa nào gấp được hình chóp tam giác đều, hình chóp tứ giác đều?
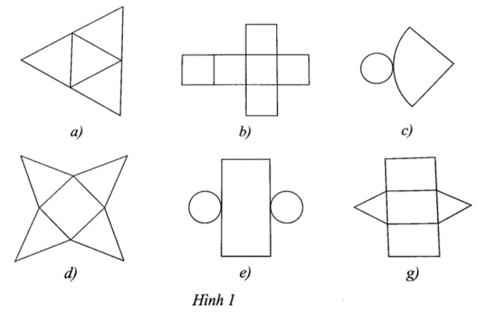
Giải
Miếng bìa ở hình 1a gấp được một hình chóp tam giác đều; miếng bìa ở hình 1d gấp được một hình chóp tứ giác đều.
Bài 9 trang 46 SBT Toán 8 tập 1 CTST: Tính diện tích xung quanh của hình chóp tam giác đều có cạnh đáy 2,3 cm và chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tam giác đều bằng 2,5 cm.
Giải
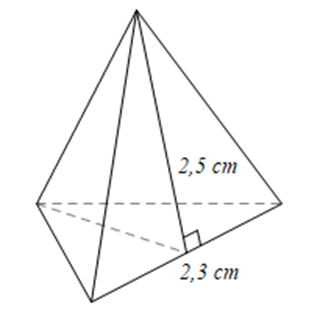
Diện tích xung quanh của hình chóp tam giác đều là:
Bài 10 trang 46 SBT Toán 8 tập 1 CTST: Tính diện tích toàn phần của hình chóp tứ giác đều có cạnh đáy 25 m và chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều bằng 20 m.
Giải
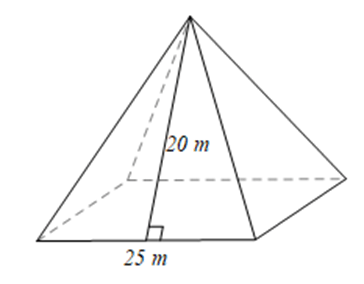
Diện tích toàn phần của hình chóp tứ giác đều là:
$S_{tp} = S{xq} + S_{day} = 4. \frac{25.20}{2} + 25^{2} =1625 ( m^{2})$
Bài 11 trang 46 SBT Toán 8 tập 1 CTST: Một mái che giếng trời có dạng hình chóp tứ giác đều (Hình 2) cạnh đáy 2,5 m, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều bằng 2,2 m.
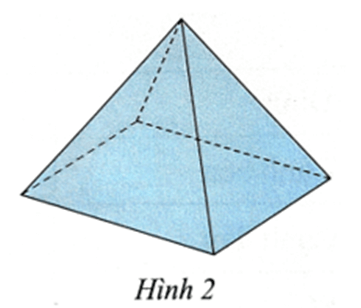
a) Tính diện tích xung quanh của mái che.
b) Chi phí cho mỗi mét vuông mái che bằng kính là 2 triệu đồng. Hỏi chi phí để hoàn thành mái che là bao nhiêu?
Giải
a) Diện tích xung quanh của mái che là:
$S_{xq} = 4. \frac{2,5 . 2,2 }{2} =11 m^{2}$
Bài 12 trang 46 SBT Toán 8 tập 1 CTST: Một chiếc gàu có dạng hình chóp tứ giác đều và một chiếc bình có dạng hình lăng trụ đứng tứ giác có cùng diện tích đáy. Người ta múc đầy 10 gàu nước và đổ vào bình. Hỏi mực nước trong bình tăng thêm bao nhiêu? Cho biết chiều cao của chiếc gàu là 0,3 m.
Giải
Gọi diện tích đáy của chiếc gàu (cũng là diện tích đáy của chiếc bình) là S, thể tích của chiếc gàu là V, số đo của mực nước tăng thêm là h. Khi đó:
thể tích của 1 gàu nước là:
$\frac{1}{3} .S , 0,3 = 0,1S m^{3}$
thể tích của 10 gàu nước là
10 . 0,1S = S (m3).
thể tích của nước đổ vào bình là: Sh (m3).
Do đó S = Sh, suy ra h = 1 (m).
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây

Bình luận