BÀI TẬP CUỐI CHƯƠNG VI

PHẦN I: HỆ THỐNG BÀI TẬP CUỐI SGK

Bài 6.24: Tập xác định của hàm số y= là:

A. D = [2;+∞)                              B. D =  (2;+∞)   

C. R∖2                                       D. D = R

Bài 6.25:  Parabol y=x²+2x+3 có đỉnh là:

A. I(-1; 0)              B. I(3; 0)

C. I(0; 3)               D. I(1; 4)

Bài 6.26: Hàm số y=x²−5x+4

A. Đồng biến trên khoảng (1;+∞).          B. Đồng biến trên khoảng (−∞;4). 

C. Nghịch biến trên khoảng (−∞;1)        D. Nghịch biến trên khoảng (1; 4).

Bài 6.27: Bất phương trình  y=x²−2mx+4>0 nghiệm đúng với mọi x∈R khi:

A. m = -1             B. m = -2               C. m =2                   D. m >2

Bài 6.28 : Tập nghiệm của phương trình là:

A. {-1-}                  B. {-1-}  

C. {-1+}                                 D. ⊘ 

Bài 6.29: Tìm tập xác định của các hàm số sau:

a)

b)

Bài 6.30: Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tìm tập giá trị , khoảng biến thiên, khoảng đồng biến, khoảng nghịch biến của nó:

a)

b) 

c) 

d) 

Bài 6.31: Xác định parabol (P): y=ax²+bx+3 trong mỗi trường hợp sau:

a. (P) đi qua hai điểm A(1; 1) và B(-1; 0)

b. (P) đi qua hai điểm M(1; 2) và nhận đường thẳng x =1 làm trục đối xứng.

c. (P) có đỉnh là I(1; 4)

Bài 6.32: Giải các bất phương trình sau:

a)

b)

c)

d)

Bài 6.33: Giải các phương trình sau:

a)                         b)

Bài 6.34: Một công ty bắt đầu sản xuất và bán một loại máy tính xách tay từ năm 2018. Số lượng loại máy tính đó bán được trong hai năm liên tiếp 2018 và 2019 lần lượt là 3,2 nghìn và 4 nghìn chiếc. Theo nghiên cứu dự báo thị trường của công ty, trong khoảng 10 năm kể từ năm 2018, số lượng máy tính loại đó bán được mỗi năm có thể được xấp xỉ bởi một hàm bậc hai.

Giả sử t là thời gian (theo đơn vị năm) tính từ năm 2018. Số lượng loại máy tính đó bán được trong năm 2018 và năm 2019 lần lượt được biểu diễn bởi các điểm (0; 3,2) và (1; 4). Giả sử điểm (0; 3,2) là đỉnh đồ thị của hàm số bậc hai này.

a. Lập công thức của hàm số mô tả số lượng máy tính xách tay bán được qua từng năm.

b. Tính số lượng máy tính xách tay đó bán được trong năm 2024.

c. Đến năm bao nhiêu thì số lượng máy tính xách tay đó được bán trong năm sẽ vượt mức 52 nghìn chiếc?

PHẦN II: 5 PHÚT GIẢI BÀI TẬP CUỐI SGK

Bài 6.24:  

B

Bài 6.25:  

D

Bài 6.26: 

C

Bài 6.27: 

A

Bài 6.28 : 

C

Bài 6.29: 

a)

b)

Bài 6.30: 

a) 

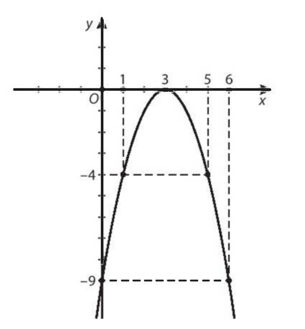
+) Tập giá trị:

+) Hàm số đồng biến trên khoảng và nghịch biến trên khoảng .

b) 

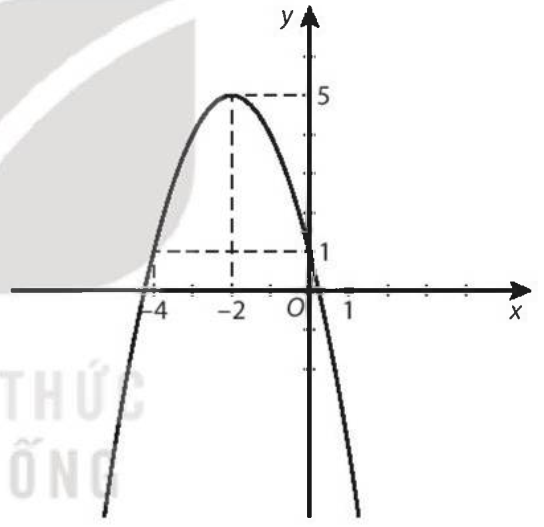
+) Tập giá trị:

+) Hàm số đồng biến trên khoảng và nghịch biến trên khoảng .

c) 

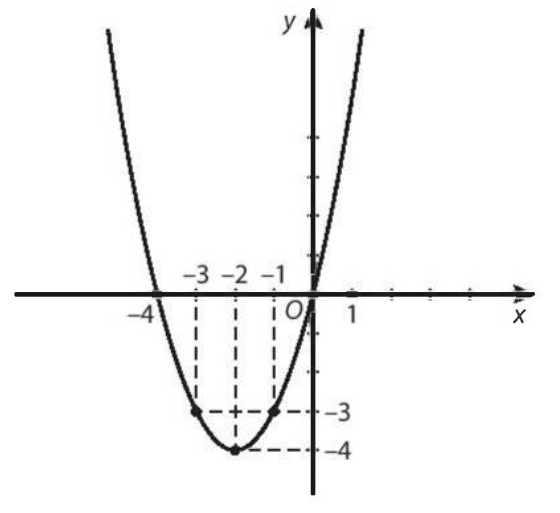
+) Tập giá trị:

+) Hàm số đồng biến trên khoảng và nghịch biến trên khoảng .

d) 

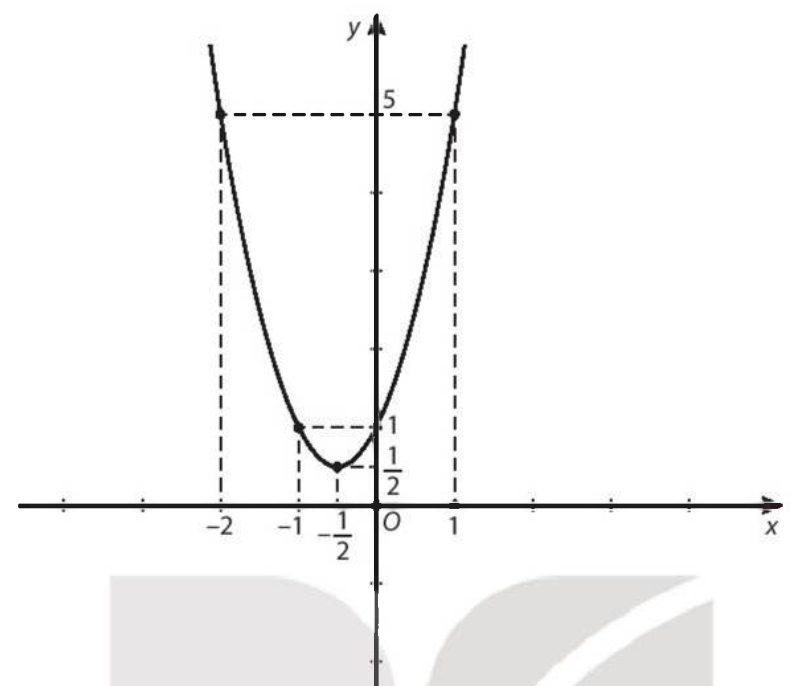
+) Tập giá trị:

+) Hàm số đồng biến trên khoảng và nghịch biến trên khoảng .

Bài 6.31: 

a)

b) .

c) .

Bài 6.32: 

a)

b)

c)

d) vô nghiệm

Bài 6.33: 

a)

b)

Bài 6.34: 

a)

b)

c) 2026