Soạn giáo án điện tử toán 7 chân trời bài 4: Diện tích xung quanh của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác (2 tiết)

Nội dung giáo án

THÂN MẾN CHÀO CÁC EM ĐẾN VỚI BÀI HỌC HÔM NAY!

KHỞI ĐỘNG

KHỞI ĐỘNG

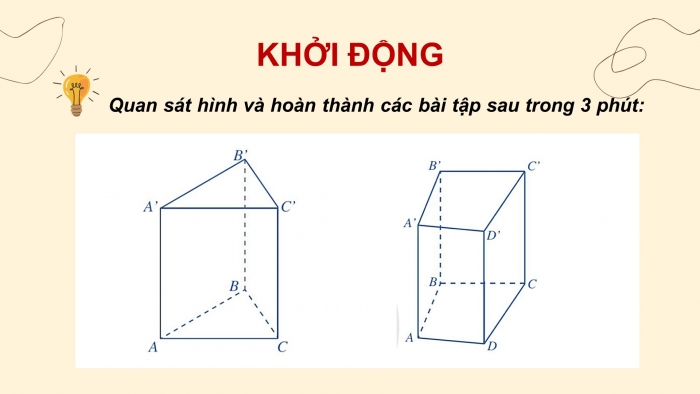
Quan sát hình và hoàn thành các bài tập sau trong 3 phút:

Bài 1. Tìm số thích hợp điền vào ô trống trong bảng sau:

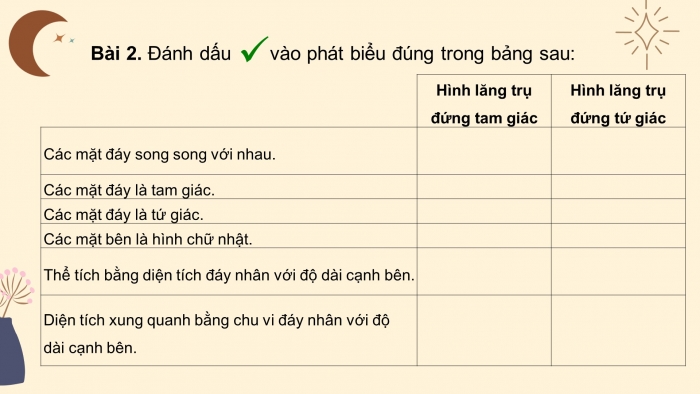
Bài 2. Đánh dấu       vào phát biểu đúng trong bảng sau:

BÀI 4: DIỆN TÍCH XUNG QUANH CỦA HÌNH LĂNG TRỤ ĐỨNG TAM GIÁC, LĂNG TRỤ ĐỨNG TỨ GIÁC (2 Tiết)

NỘI DUNG BÀI HỌC

Diện tích xung quanh của hình lăng trụ đứng

Thể tích của hình lăng trụ đứng

Diện tích xung quanh và thể tích của một số hình khối trong thực tiễn

1. Diện tích xung quanh của hình lăng trụ đứng

Quan sát và hoạt động nhóm 4 để thực hiện HĐKP1.

HĐKP1

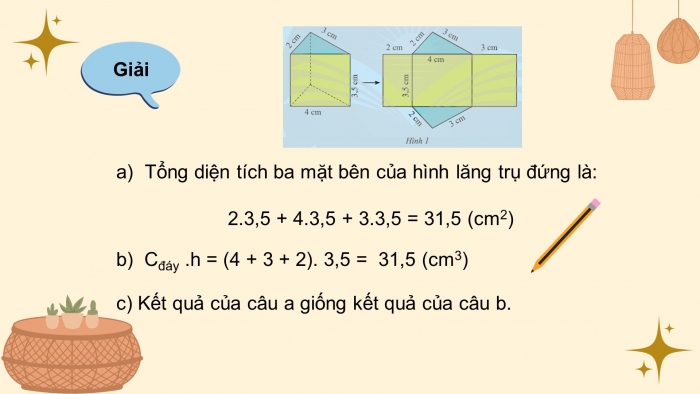
Hãy quan sát lăng trụ đứng tam giác (Hình 1) và thực hiện các yêu cầu sau:

1. Tính tổng diện tích ba mặt bên của hình lăng trụ đứng.
2. Gọi C_đáy là chu vi đáy và h là chiều cao của hình lăng trụ, tính C_đáy. h.
3. So sánh kết quả của câu a và b.

Giải

1. Tổng diện tích ba mặt bên của hình lăng trụ đứng là:

 2.3,5 + 4.3,5 + 3.3,5 = 31,5 (cm²)

1. b)  C_đáy.h = (4 + 3 + 2). 3,5 =  31,5 (cm³)
2. c) Kết quả của câu a giống kết quả của câu b.

KẾT LUẬN

Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao.

S_xq = C_đáy . h

(C_đáy là chu vi đáy, h là chiều cao)

Chú ý: Diện tích toàn phần của lăng trụ đứng bằng tổng diện tích xung quanh và diện tích hai đáy.

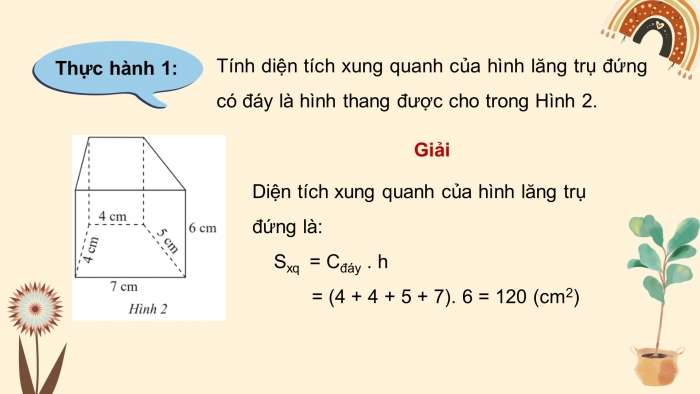
Thực hành 1:

Tính diện tích xung quanh của hình lăng trụ đứng có đáy là hình thang được cho trong Hình 2.

Giải

Diện tích xung quanh của hình lăng trụ đứng là:

    S_xq  = C_đáy . h

           = (4 + 4 + 5 + 7). 6 = 120 (cm²)

2. Thể tích của hình lăng trụ đứng

Hoạt động nhóm thực hiện lần lượt các yêu cầu HĐKP2.

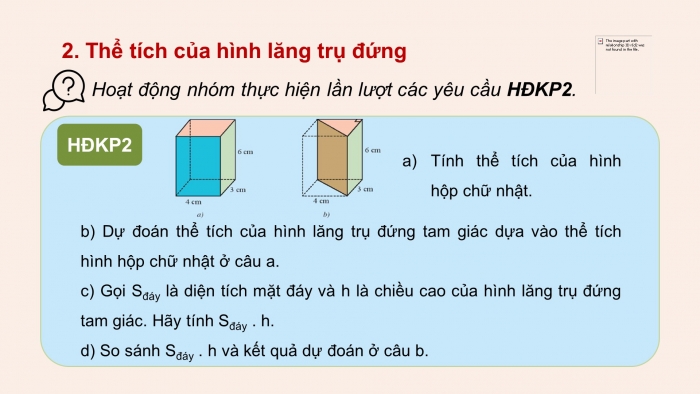
HĐKP2

1. Tính thể tích của hình hộp chữ nhật.
2. b) Dự đoán thể tích của hình lăng trụ đứng tam giác dựa vào thể tích hình hộp chữ nhật ở câu a.
3. c) Gọi S_đáy là diện tích mặt đáy và h là chiều cao của hình lăng trụ đứng tam giác. Hãy tính S_đáy . h.
4. d) So sánh S_đáy . h và kết quả dự đoán ở câu b.

Giải

4. a) Thể tích của hình hộp chữ nhật là: V = 4.3.6 = 72 (cm³)
5. b) Vì hình hộp cắt đi một nửa thì được hình lăng trụ đứng dự đoán thể tích của hình lăng trụ đứng tam giác bằng một nửa thể tích hình hộp chữ nhật ở câu a.
6. c) S_đáy= . 4. 3 = 6 (cm²)

   S_đáy. h = 6. 6 = 36 (cm³)

1. d) S_đáy. h = 36 = .V_{hình hộp}

Vậy S_đáy. h và kết quả dự đoán ở câu b là như nhau.

KẾT LUẬN

Thể tích của hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao.

V = S_đáy. h

(S_đáy là diện tích đáy, h là chiều cao)

• Trong HĐKP2, đối với trường hợp đáy là một tam giác không vuông, ta có thể chọn đỉnh có góc lớn nhất rồi vẽ đường cao của tam giác ở đáy.
• Khi đó tam giác ở đáy được chia thành hai tam giác vuông và thể tích của hình lăng trụ đứng bằng tổng thể tích của hai hình lăng trụ thành phần có đáy là tam giác vuông.
• Công thức thể tích vẫn là V = S.h. Đối với đáy là một đa giác bất kì cũng có thể dùng cách thực hiện tương tự.

Ví dụ 2: Thể tích của hình lăng trụ đứng tam giác trong HĐKP2 là:         V = S_đáy. h = . 6 = 36 (cm³)

Thảo luận cặp đôi áp dụng công thức hoàn thành Thực hành 2

Tính diện tích xung quanh của một cột trụ bê tông hình lăng trụ đứng có chiều cao 2 m và đáy là tam giác đều có cạnh 0,5 m (Hình 4).

Giải

Diện tích xung quanh của cột bê tông đó là:

S_xq = C_đáy. h = (0,5 + 0,5 + 0,5). 2 = 3 (m²)

Thực hành 3

Tính thể tích lăng trụ đứng tứ giác có đáy là hình thang với kích thước cho trong Hình 5.

Giải

Diện tích đáy của lăng trụ là:

S_đáy = (5 + 8). 4 : 2 = 26 (cm²)

Thể tích hình lăng trụ đứng trong Hình 5 là:

V = S_đáy. h = 26 . 12 = 312 (cm³)

3. Diện tích xung quanh và thể tích của một số hình khối trong thực tiễn

Ví dụ 3: Hình 6 là tấm lịch để bàn có dạng hình lăng trụ đứng tam giác. Tính diện tích xung quanh của tấm lịch.

Giải

Diện tích xung quanh của tấm thiệp để bàn là:

S_xq = C_đáy. h = (7 + 15 + 15). 16

                                  = 37. 16 = 592 (cm²)

Ví dụ 4: Gàu xúc của một xe xúc (Hình 7a) có dạng gần như một hình lăng trụ đứng tam giác với kích thước đã cho trong Hình 7b. Để xúc hết 40 m³ cát, xe phải xúc ít nhất bao nhiêu gàu?

Giải

Thể tích của gàu xúc hình lăng trụ là:

V = S_đáy. h = . 1,2. 1. 3,2 = 1,92 (m²)

Ta có:  = 20

Vậy xe phải xúc ít nhất 21 gàu để hết 40 m³ cát.

Trao đổi nhóm đôi hoàn thành Thực hành 4

Thực hành 4

Để làm đường dẫn lên cầu bắc qua một con kênh, người ta đúc một khối bê tông hình lăng trụ đứng tam giác có kích thước như Hình 8. Hãy tính thể tích khối bê tông.

Giải

Thể tích khối bê tông là:

V = S_đáy . h  = . 24. 7. 22 = 1 848 (m³)

Vận dụng

Bạn Nam đã làm một chiếc hộp hình lăng trụ đứng với kích thước như Hình 9. Bạn ấy định sơn các mặt của chiếc hộp, trừ mặt bên dưới. Hãy tính diện tích cần sơn.

Giải

Chiếc hộp hình lăng trụ có 2 đáy là hình thang và các mặt bên là hình chữ nhật.  Diện tích xung quanh chiếc hộp là:

S_xq = C_đáy. h = (6 + 4 + 8 + 4 + 10). 3 = 96 (cm²)

Diện tích 2 đáy là: S_2đáy = (10 + 4). 8: 2. 2 = 112 (cm²)

Các mặt cần sơn gồm hai mặt đáy và 3 mặt bên (trừ mặt bên dưới) 

 Diện tích phần cần sơn là: 96 + 112 – 8. 3 = 184 (cm²)

LUYỆN TẬP

Bài 1 (SGK - tr62)

Một chiếc hộp đèn có dạng hình lăng trụ đứng tam giác có kích thước như Hình 10. Tính diện tích xung quanh của chiếc hộp.

Giải

Diện tích xung quanh của chiếc hộp là:

S_xq = C_đáy. h = (20 + 12 + 16). 25 = 1 200 (cm²)

Bài 4 (SGK - tr63)

Tính thể tích hình lăng trụ đứng có đáy là hình thang cân với kích thước như Hình 13.

Giải

Diện tích đáy là: .(8 + 4).3 = 18 (cm²)

Thể tích lăng trụ đứng là:

V = S_đáy. h = 18.9 = 162 (cm³)

Bài 6 (SGK - tr63)

Một hình lăng trụ đứng tứ giác có kích thước đáy như Hình 15, biết chiều cao của lăng trụ là 7cm. Tính thể tích của hình lăng trụ.

Giải

Diện tích đáy của lăng trụ là:

3. 6 + . 4. 6 = 21 (cm²)

Tính thể tích lăng trụ đứng là:

V = S_đáy. h = 21. 7= 147 (cm³)

VẬN DỤNG

Bài 2 (SGK - tr62)

Một chiếc lều trại có hình dạng và kích thước như Hình 11. Tính tổng diện tích tấm bạt có thể phủ kín toàn bộ lều (không tính mặt tiếp giáp với đất) và thể tích chiếc lều.

Giải

Diện tích tấm bạt có thể phủ kín toàn bộ lều (không tính mặt tiếp giáp với đất) là:

S = S_xq + S_đáy = (4 + 2,5 + 2,5).6 +  . 4. 1,5 = 57 (m²)

Thể tích của chiếc lều là:

V = S_đáy . h =  . 4. 1,5. 6 = 12 (m³)

Bài 3 (SGK - tr62): Một cái bục hình lăng trụ đứng có kích thước như Hình 12.

1. Người ta muốn sơn tất cả các mặt của cái bục. Diện tích cần phải sơn là bao nhiêu?
2. Tính thể tích của cái bục.
3. a) Diện tích xung quanh của lăng trụ là: (4 + 8 + 5 + 5). 12 = 264 (dm²)

Diện tích đáy của lăng trụ là: . (5 + 8).4 = 26 (dm²)

Diện tích cần sơn là: S_xq + 2. S_đáy = 264  + 2. 26 = 316 (dm²)

26. b) Thể tích bục là: V = S_đáy. h = 26. 12 = 312 (dm³)

Bài 5 (SGK - tr63): Để làm đường dẫn bắc ngang một con đê, người ta đúc một khối bê tông có kích thước như Hình 14. Tính chi phí để đúc khối bê tông đó, biết rằng chi phí để đúc một 1 m³ bê tông là 1,2 triệu đồng.

Giải

Diện tích đáy hình thang là: (2 + 2 + 9). 4 : 2 = 26 (m²)

Thể tích khối bê tông đó là:

V = S_đáy. h = 26. 6 = 156 (m³)

Chi phí để đúc khối bê tông đó là:

156. 1,2 = 187,2 (triệu đồng)

HƯỚNG DẪN VỀ NHÀ

Ghi nhớ các kiến thức đã học

Hoàn thành bài tập trong SBT

Chuẩn bị bài sau “Bài 5. Hoạt động thực hành và trải nghiệm: Các bài toán đồ đạc và gấp hình”

CẢM ƠN CÁC EM ĐÃ CHÚ Ý LẮNG NGHE!