Giải luyện tập 2 trang 115 sgk Toán 8 tập 1 CD

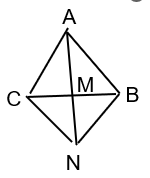
Xét 2 tam giác AMC và NMB có: 

• AM = NM (gt)
• MC = MB (M là trung điểm của BC)
• $\widehat{AMC}=\widehat{NMB}$ (2 góc đối đỉnh)

=> 2 tam giác AMC và NMB bằng nhau theo trường hợp c-g-c.=> 2 cạnh tương ứng BN = AC (1)

Xét 2 tam giác AMB và NMC có: 

• AM = NM (gt)
• MC = MB (M là trung điểm của BC)
• $\widehat{AMB}=\widehat{NMC}$ (2 góc đối đỉnh)

=> 2 tam giác AMB và NMC bằng nhau theo trường hợp c-g-c.=> 2 cạnh tương úng AB = CN (2)

Mà ABC cân tại A nên AB = AC (3)

Từ (1), (2), (3) => AB = AC = BN  = NC => Tứ giác ABNC có 4 cạnh bằng nhau nên là hình thoi.