Giải hoạt động 2 trang 113 sgk Toán 8 tập 1 CD

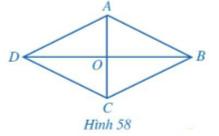
a) ABCD là hình thoi nên AB=BC=CD=DA . Suy ra:

2 tam giác DAB và DCB bằng nhau (c-c-c) => Góc A và góc C bằng nhau. 

2 tam giác DAC và BAC bằng nhau (c-c-c) => Góc D và góc B bằng nhau. 

=> Tứ giác ABCD có 2 cặp góc đối bằng nhau nên là hình bình hành. 

b) Từ a, ABCD là hình bình hành nên O là trung điểm của mỗi đường chéo. 

Xét 2 tam giác AOB và AOD có: 

• OA chung
• OB = OA
• AD = AB

=> 2 tam giác AOB và AOD bằng nhau. => $\widehat{AOD}=\widehat{AOB}$. mặt khác chúng lại là 2 góc bù nhau nên $\widehat{AOD}=\widehat{AOB}$ = $90^{\circ}$

=> Hai đường chéo AC và BD có vuông góc với nhau

c) Hai tam giác ABC và ADC có:

• AC chung
• AB=AD
• BC=DC

=> Hai tam giác ABC và ADC bằng nhau theo trường hợp c-c-c.

=> 2 góc tương ứng là BAC và DAC bằng nhau => AC là tia phân giác của góc BAD.