Giải câu 4 đề 8 ôn thi toán lớp 9 lên 10

Hình vẽ:

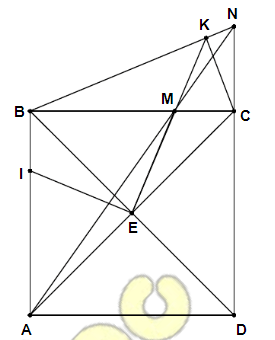
a. Tứ giác BIEM có: $\widehat{IBM}=\widehat{IEM}=90^{0}$ (gt); suy ra tứ giác BIEM nội tiếp đường tròn đường kính IM.

b. Tứ giác BIEM nội tiếp suy ra: $\widehat{IME}=\widehat{IBE}=45^{0}$ (do ABCD là hình vuông)

c. $\Delta EBI$ và $\Delta ECM$ có:

$\widehat{IBE}=\widehat{MCE}=45^{0}$

$BE = CE$

$\widehat{BEI}=\widehat{CEM}$

$\widehat{IEM}=\widehat{BEC}=90^{0}$

$\Rightarrow \Delta EBI=\Delta ECM (g.c.g)\Rightarrow MC =IB$, suy ra $MB = IA$

Vì: CN// BA nên theo định lí thalet, ta có:

$\frac{MA}{MN}=\frac{MB}{MC}=\frac{IA}{IB}$ Suy ra IM song song với BN (định lí thalet đảo).

$\Rightarrow \widehat{BKE}=\widehat{IME}=45^{0} (2)$. Lại có $\widehat{BCE}=45^{0}$ (do ABCD là hình vuông).

Suy ra: $\widehat{BKE}=\widehat{BCE}\Rightarrow BKCE$ là tứ giác nội tiếp.

Suy ra: $\widehat{BKC}+\widehat{BEC}=180^{2}$ mà $\widehat{BEC}=90^{0}$, suy ra $\widehat{BKC}=90^{2}$ hay $CK\perp BN$.