Giải Bài tập 9 trang 89 sgk Toán 8 tập 1 Chân trời

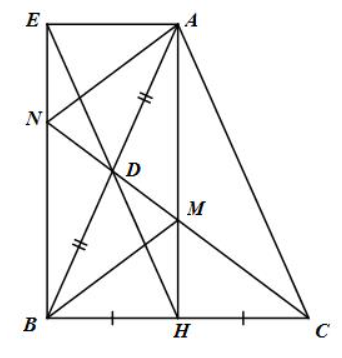
a) Ta có D, H lần lượt là trung điểm của AB và BC.

⇒DH là đường trung bình của tam giác ABC.

⇒DH//AC⇒ Tứ giác ADHC là hình thang.

b) ΔABC cân tại A có AH là đường trung tuyến (H là trung điểm của BC)

⇒AH là đường cao của tam giác ABC.

⇒AH⊥BC tại H.

Tứ giác AHBE có AB và EH cắt nhau tại D (gt)

D là trung điểm của AB (gt)

D là trung điểm của EH (E là điểm đối xứng với H qua D),

$\widehat{NED}=\widehat{DHM}$ (hai góc so le trong và EB // AH)

Và $\widehat{EDN}=\widehat{HDM}$  (hai góc đối đỉnh), do đó ΔEND=ΔHDM(g.c.g)

⇒ND=MD⇒Dlà trung điểm của NB (D∈NM)

Mặt khác D là trung điểm của AB (gt) và NM, AB cắt nhau tại D (gt)

Do đó tứ giác AMBN là hình bình hành (dấu hiệu nhận biết hình bình hành)