Giải Bài tập 8 trang 89 sgk Toán 8 tập 1 Chân trời

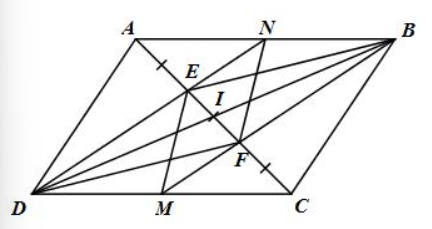
a) Gọi I là tâm đối xứng của hình bình hành ABCD

⇒I là trung điểm của AC và BD ⇒IA=IC

⇒IA–AE=IC–FC (vì AE=FC)

⇒EI=FI⇒I là trung điểm của EF.

Tứ giác DEBF có DB và EF cắt nhau tại I (I là tâm đối xứng, E,F∈AC)

I là trung điểm của BD và I là trung điểm của EF.

Do đó tứ giác DEBF là hình bình hành

⇒DE//BF⇒EN//BF(N∈DE)

Mà E là trung điểm của AF (AE=EF) nên N là trung điểm của AB.

ΔDEC có MF//DE(DE//BF,M∈BF) và F là trung điểm của EC (EF=FC)

⇒M là trung điểm của CD.

b) Ta có

AN=$\frac{AB}{2}$ (N là trung điểm của AB)

MC=$\frac{CD}{2}$ (M là trung điểm của CD)

AB=CD (ABCD là hình bình hành)

⇒AN=MC

Xét tam giác AEN và tam giác MFC ta có :

AE=FC(gt)

AN=MC (gt)

$\widehat{NAE}=\widehat{FCM}$ (hai góc so le trong và AB // CD)

Do đó ΔAEN=ΔCFM(c.g.c)

Tứ giác EMFN có EN // MF (DE//BF,N∈DF,M∈BF)

Và EN=MF(ΔAEN=ΔCFM). Do đó tứ giác EMFN là hình bình hành.