Giải Bài tập 11 trang 89 sgk Toán 8 tập 1 Chân trời

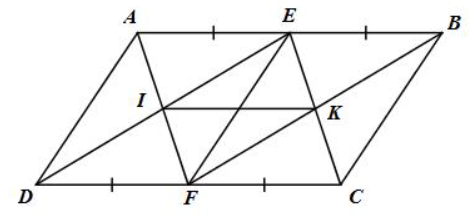
a) Ta có $AE=EB=\frac{AB}{2}$ (E là trung điểm của AB),

$DF=FC=\frac{CD}{2}$ (F là trung điểm của CD)

Và AB=CD(ABCD là hình bình hành)

⇒AE=CF=EB=DF

Tứ giác AECF có AE // CF (AB // CD, E∈AB,F∈CD) và AE=CF

⇒AECF là hình bình hành.

b) Ta có : AB=2AD(gt) và AB=2AE  (E là trung điểm của AB) => AD = AE

Tứ giác AEFD có AE // DF và AE=DF(chứng minh câu a)

⇒ Tứ giác AEFD là hình bình hành

Mà AE=AD (chứng minh trên) nên AEFD là hình thoi.

c) Ta có AF⊥DE tại I (AEFD là hình bình hành)

Và AF//EC(AECF là hình bình hành) ⇒EC⊥DE⇒$\widehat{IEK}=90^{\circ}$

Ta có EF=AE(AEFD là hình thoi)

Và AE=$\frac{1}{2}AB$ (E là trung điểm của AB) ⇒EF=$\frac{1}{2}AB$

ΔAFBcó FE là đường trung tuyến (E là trung điểm của AB) và EF=$\frac{1}{2}AB$

⇒ΔAFB vuông tại F ⇒$\widehat{IFK}=90^{\circ}$

Tứ giác EIFK có :

$\widehat{EIF}=90^{\circ}$ (IE⊥IFtại I)

$\widehat{IEK}=90^{\circ}$

$\widehat{IFK}=90^{\circ}$

Do đó tứ giác EIFK là hình chữ nhật.

d) Ta có tứ giác EIFK là hình chữ nhật.

I là trung điểm của ED (tứ giác AEFD là hình bình hành)

Tương tự K là trung điểm của EC.

Do đó IK là đường trung bình của tam giác ECD ⇒IK⊥CD

Mặt khác AD // EF (tứ giác AEFD là hình bình hành)

Do đó tứ giác EIFK là hình vuông.

⇔ Hình chữ nhật EIFK có IK⊥EF⇔IK⊥AD⇔AD⊥CD

⇔ Hình bình hành ABCD có $\widehat{ADC}=90^{\circ}$

Vậy điều kiện của hình bình hành ABCD là $\widehat{ADC}=90^{\circ}$ để tứ giác EIFK là hình vuông.