Giải bài tập 88 trang 94 SBT toán 7 tập 2 cánh diều

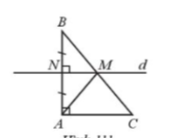
Gọi d là đường trung trực của cạnh AB và M là giao điểm của d và BC.

Do $M\in d$ nên MA = MB hay tam giác MAB cân tại M. Suy ra $\widehat{MBA}=\widehat{MAB}$

Ta có $90^{\circ}-\widehat{MBA}=90^{\circ}-\widehat{MAB}$ hay $\widehat{MAC}=\widehat{MCA}$.

Do đó tam giác MAC cân tại M.

Suy ra MA = MC

Như vậy, MA = MB = MC.

Vậy các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.